Arabesques
| Wheelies | Interlude | Deep Dive | From Wheelies, Arabesques |
| From Arabesques, Wheelies | Wheelie Animations |
"Durga's idle arabesques" | During brief interludes, when tranquility prevails and the peoples of the world are in complete accord, Durga might take ease from her duties and find serenity through simple pursuits. It is a small pleasure to swing a compass marker around its anchor leg, and if hands might quave arcs still run true — not that palsy ever troubles Durga, master as she is of the chakra and trishul. And so it is hardly burdensome for her to take up compass after compass, anchor to marker, twirling each at spins and spreads picked through whimsy. Such a flurry of hands and arms might astonish mortals, but for the slayer of the abominable Mahishasura it is just so many twirlings. With each added compass, the culminating marker traces ways ever more sublime, awarding Durga escalating delights. And so it goes — until demons arise. Durga must then put away her compasses and take up her arrows and bow. |
Wheelies
Deficient as we are in arms, we seek computerized compensations. Accordingly, let wheelies model compass pairs: one end of a segment is a hinge that sticks to whatever it has been attached and the other end swings free. Chains of these emulate Durga's compass-upon-compass pile-ons.Roughly, we'd like to have some command, gtutor_wheelie — which we don't know how to write yet. But let's imagine it lives in a place called scripts/wheelie_simple.gmic and can draw simple arabesques:
 |  |  |
| simple | threewheelie | colorwheelie |
This would produce a two-wheelie arabesque:
simple:
-command scripts/wheelie_simple.gmic
-input 300,300,1,1
-gtutor_wheelie. 0.375,0,1,0.375,0,2
-output. simple.png
-command scripts/wheelie_simple.gmic
-input 300,300,1,1
-gtutor_wheelie. 0.375,0,1,0.375,0,2
-output. simple.png
0.375,0,1 specifies a wheelie with a radius (length) of 0.375, an initial orientation of 0° and a rotational rate of one counterclockwise revolution per period — a "frequency" of one cycle — aka one Hertz. The second wheelie, 0.375,0,2 is almost the same as the first but rotates at twice the frequency.
Now: add a third wheelie for more sublime twirlings:
threewheelie:
-command scripts/wheelie_simple.gmic
-input 1024,1024,1,1
-gtutor_wheelie 0.375,0,1,0.3125,0,2,0.25,0,5
-dilate_circ 4
-resize2dx. 300,5
-output. threewheelie.png
-command scripts/wheelie_simple.gmic
-input 1024,1024,1,1
-gtutor_wheelie 0.375,0,1,0.3125,0,2,0.25,0,5
-dilate_circ 4
-resize2dx. 300,5
-output. threewheelie.png
Perhaps you find white-on-black plain. Of course it's plain. A separation of concerns is at work here. gtutor_wheelie does wheelies. It draws white on black and that's that. It leaves fancier rendering to G'MIC commands better suited for such embellishment, such as colorwheelie mappings:
colorwheelie :
-command scripts/wheelie_simple.gmic
-input 1024,1024,1,1
-gtutor_wheelie. 0.375,0,1,0.3125,0,2,0.25,0,5,0.0625,57,-6,0.03125,85,-11
-name arab
-dilate_circ[arab] 4
-label[arab]
-normalize[arab] 0,255
# 1D Radial Basis Function - key points: x,r,g,b
-input (0,70,70,90^10,-10,-10,-10^95,40,200,215^175,255,235,60^255,220,40,30)
-name keys
# Pack keypoints into 4 channel pixels: X,R,G,B
-permute[keys] cyzx
-rbf[keys] 255
-name. palette
-normalize[palette] 0,255
-map[arab] [palette]
-keep[arab]
-resize2dx[arab] 300,5
-output[arab] colorwheelie.png
-command scripts/wheelie_simple.gmic
-input 1024,1024,1,1
-gtutor_wheelie. 0.375,0,1,0.3125,0,2,0.25,0,5,0.0625,57,-6,0.03125,85,-11
-name arab
-dilate_circ[arab] 4
-label[arab]
-normalize[arab] 0,255
# 1D Radial Basis Function - key points: x,r,g,b
-input (0,70,70,90^10,-10,-10,-10^95,40,200,215^175,255,235,60^255,220,40,30)
-name keys
# Pack keypoints into 4 channel pixels: X,R,G,B
-permute[keys] cyzx
-rbf[keys] 255
-name. palette
-normalize[palette] 0,255
-map[arab] [palette]
-keep[arab]
-resize2dx[arab] 300,5
-output[arab] colorwheelie.png
So let's set about to write gtutor_wheelie.
With each wheelie we may:
| 1. | set a particular radius: | +r |
| 2. | pick a starting orientation: | ±θ |
| 3. | choose a signed, clockwise or counterclockwise, rotational rate: | ± 2πf |
Thus, to make a wheelie chain ( Figure 1 ):
| 1. | Root the first wheelie at the origin. |
| 2. | Hinge additional wheelies at successive free end points, perhaps setting their orientation differently or aligning them all. Do that any number of times, or |
| 3. | attach a marker to the rim of a terminal wheelie and take a picture of the pip it draws. |
| 4. | Adjust the orientations to account for 2πf(Δt) angular accretion and plot again … and again until the accumulated adjustment equals some preset, perhaps a full circular rotation of 2π, anticipating that that period draws one arabesque from start to finish. What remains is the traversal path of the marker in all of its charm — an arabesque. |
Plot by plot, a wheelie's circular motion fathoms easily. But add a few more — complexity strikes us dumb. The remedy for that are patterns. These, in recurrence, divide and conquer.
| 1. Walking a wheelie chain from marker tip to the origin |
Let paired wheelies, antecedent and successor, provide the exemplary pattern. First, characterize relative motion in the locality of a wheelie pair. Then aggregate motions of pairs into larger localities — ultimately that of the whole chain.
Start with the next-to-the-last and final wheelie. Establish a local coordinate system encompassing this last pair. Orient the antecedent to zero degrees, anchor at the local origin and tip aligned with the local x axis. Now bring in the successor. It's sticky end hinges to the antecedent's tip while its own swings free.
The factors accounting for the successor's local motion with respect to its antecedent are its length, r, and its orientation θ. To the orientation add the dynamic angle: 2πft, the product of the successor's rotational rate 2πf and accumulated ticks: t = ( Δt₀ + Δt₁ + … ).
These factors bring about an affine matrix, one that takes a point in the neighborhood of the successor's origin (née antecedent's tip) through a translation by r and a rotation by 2πft + θ :
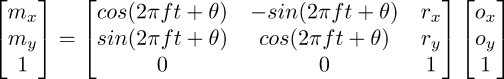
2. A Wheelie transform taking a point at o (origin) to m (tip)
This matrix characterizes motion in the locality of this wheelie pair. As Δt ticks accumulate, changing 2πft, the tip traces a circle of radius r; not very interesting but readily grasped.
| 3. The locality of one wheelie pair |
| 4. Localities of the second and third, and first and second wheelie pairs compounded together |
| 5. Localities of three wheelies of rates one, two and three |
We mark one plot and tick Δt. That changes the orientation of all wheelies, of course, so we re-walk the walk, compound the adjusted matrices and plot the second mark. And again. And again … until the preset has been reached; perhaps a full revolution of the first, or root wheelie.
After all that — we're done. We know how to write this gtutor_wheelie script. The implementation looks something like wheelie_simple.gmic. Unroll it for details. See Annotations for the weeds.
( Download wheelie_simple.gmic ):
wheelie_simple.gmic
1 #@cli gtutor_wheelie : radius₀>0,–∞<orientation₀<+∞,-∞<rotrate₀<+∞…
2 #@cli : Compose an arabesque from a chain of wheelies; specify each
3 #@cli : link with triplets: radius (+float), orientation (±degrees,
4 #@cli : float), rotational rate (±integer) and draw on the selected
5 #@cli : images. A wheelie is a tail-anchored rotating vector of a
6 #@cli : particular (1) radius, (2) phase angle (orientation) and (3)
7 #@cli : discrete rotational rate, some relative integral number of
8 #@cli : revolutions per an unspecified period. Wheelies chain
9 #@cli : together, the center of one situated at the 0° mark on the
10 #@cli : rim of its antecedent. The first wheelie of the chain
11 #@cli : centers on the origin and the last has attached instead of
12 #@cli : another wheelie, a marking pen. Thus, the entire ensemble
13 #@cli : draws an "arabesque" as the individual wheelies rotate at
14 #@cli : their respective rotational rates and from their initial
15 #@cli : orientations.
16 #@cli : $ gmic 1024,1024,1,1 gtutor_wheelie. 0.5,67,1,0.25,0,-3 name. tricirc
17
18 gtutor_wheelie:
19 # Fetch an arbitrarily long argument list to $a0, $a1, …, $an
20
21 $=a
22
23 # Expect data triplets: radius, phase angle, angular velocity.
24
25 -check "!(($#)%3)"
26
27 # Argument image: For each wheelie, compose radius and phase
28 # arguments into a transformation matrix. In the generation
29 # loop, we compose this with the angle resulting from one
30 # angular velocity step.
31
32 wcnt={int(($#)/3)}
33 -input $wcnt,1,1,12
34 -name. args
35
36 # Iterate over argument vector. For each triplet –
37 # representing a delta wheelie – Fetch radius (rad), phase
38 # angle (ang) and angular velocity (sf) parameters.
39
40 -repeat $# j=$>
41 -if $j%3==0 # get radius
42 rad=${a{1+$j}}
43 -check isnum($rad)" && "$rad>=0
44 -set[args] $rad,{round($j/3,1,-1)},0,0,0
45 -elif $j%3==1 # get angle, degrees
46 ang=${a{1+$j}}
47 -check isnum($ang)
48 -set[args] $ang,{round($j/3,1,-1)},0,0,1
49 -else # get ω and set spectral coefficient
50 sf=${a{1+$j}}
51 -set[args] $sf,{round($j/3,1,-1)},0,0,2
52 -fi
53 -done
54
55 # Iterate over argument image, each 12 channel pixel
56 # representing one wheelie. The first three channels contain
57 # wheelie radius, phase angle and radial velocity. Compose a
58 # matrix transforming the origin to the tip of the wheelie, a
59 # radial translation and phase rotation. Populate the nine
60 # remaining channels with this matrix.
61
62 -fill[args] ">
63 CPX=I;
64 orot=rot([0,0,1],deg2rad(CPX[1])); # phase rotation
65 xlat=eye(3);
66 xlat[2]=CPX[0]; # translation origin
67 [CPX[0,3,1],mul(orot,xlat,3)]; # -to-rim, i.e.
68 " # 'rotation & xlation'
69 # store above in
70 # 12-channel pixel
71 -permute[args] cyzx
72 -store[args] circles
73
74 # Screenspace transform.
75 foreach {
76 # Draw arabesques on the current image
77 # Designate it as the drawing "canvas".
78 -name. canvas
79 specw={int(min(w,h)/2)}
80 ssxfrm={"
81 sw=get('specw',0,0);
82 id=eye(3);
83 id[0]=sw;
84 id[2]=sw;
85 id[4]=-sw;
86 id[5]=sw;
87 id
88 "}
89 atk=0 # Accumulate "angular ticks"...
90 lastpt={vector3([0,0,1])}
91 firstpt={vector3([0,0,1])}
92 -repeat 3*$specw k=$> # Animation loop
93 # For each wheelie:
94 # increment by angular velocity
95 # find corresponding rotation matrix
96 # compose with radial argument image,
97 # compose with screenspace transform
98 # and plot via polygon().
99
100 -eval ">
101 const cc=$wcnt;
102 fpt=get('firstpt',3,0);
103 ik=get('k',0,0);
104 lpt=get('lastpt',3,0);
105 omega=get('atk',0,0);
106 sw=get('specw',0,0);
107 circs=get('circles',12*cc,0);
108 pp=vector3([0,0,1]);
109 imat=eye(3);
110 repeat(
111 cc,k,
112 idx=cc-k-1;
113 imat=mul(
114 mul(
115 rot([0,0,1],circs[12*idx+2]*omega),
116 circs[12*idx+3,9,1],
117 3
118 ),
119 imat,
120 3
121 );
122 );
123 ssx=get('ssxfrm',9,0);
124 plt=ssx*(imat*pp);
125 ik>0?
126 polygon(#$canvas,-2,[plt[0,2],lpt[0,2]],1,0xffffffff,255):
127 store('firstpt',plt,3,1,1,1);
128 store('lastpt',plt,3,1,1,1);
129 ik==(3*sw-1)?
130 polygon(#$canvas,-2,[fpt[0,2],plt[0,2]],1,0xffffffff,255)
131 "
132 atk={2*pi*($k/(3*$specw-1))}
133 -done #Animation loop
134 } #foreach
2 #@cli : Compose an arabesque from a chain of wheelies; specify each
3 #@cli : link with triplets: radius (+float), orientation (±degrees,
4 #@cli : float), rotational rate (±integer) and draw on the selected
5 #@cli : images. A wheelie is a tail-anchored rotating vector of a
6 #@cli : particular (1) radius, (2) phase angle (orientation) and (3)
7 #@cli : discrete rotational rate, some relative integral number of
8 #@cli : revolutions per an unspecified period. Wheelies chain
9 #@cli : together, the center of one situated at the 0° mark on the
10 #@cli : rim of its antecedent. The first wheelie of the chain
11 #@cli : centers on the origin and the last has attached instead of
12 #@cli : another wheelie, a marking pen. Thus, the entire ensemble
13 #@cli : draws an "arabesque" as the individual wheelies rotate at
14 #@cli : their respective rotational rates and from their initial
15 #@cli : orientations.
16 #@cli : $ gmic 1024,1024,1,1 gtutor_wheelie. 0.5,67,1,0.25,0,-3 name. tricirc
17
18 gtutor_wheelie:
19 # Fetch an arbitrarily long argument list to $a0, $a1, …, $an
20
21 $=a
22
23 # Expect data triplets: radius, phase angle, angular velocity.
24
25 -check "!(($#)%3)"
26
27 # Argument image: For each wheelie, compose radius and phase
28 # arguments into a transformation matrix. In the generation
29 # loop, we compose this with the angle resulting from one
30 # angular velocity step.
31
32 wcnt={int(($#)/3)}
33 -input $wcnt,1,1,12
34 -name. args
35
36 # Iterate over argument vector. For each triplet –
37 # representing a delta wheelie – Fetch radius (rad), phase
38 # angle (ang) and angular velocity (sf) parameters.
39
40 -repeat $# j=$>
41 -if $j%3==0 # get radius
42 rad=${a{1+$j}}
43 -check isnum($rad)" && "$rad>=0
44 -set[args] $rad,{round($j/3,1,-1)},0,0,0
45 -elif $j%3==1 # get angle, degrees
46 ang=${a{1+$j}}
47 -check isnum($ang)
48 -set[args] $ang,{round($j/3,1,-1)},0,0,1
49 -else # get ω and set spectral coefficient
50 sf=${a{1+$j}}
51 -set[args] $sf,{round($j/3,1,-1)},0,0,2
52 -fi
53 -done
54
55 # Iterate over argument image, each 12 channel pixel
56 # representing one wheelie. The first three channels contain
57 # wheelie radius, phase angle and radial velocity. Compose a
58 # matrix transforming the origin to the tip of the wheelie, a
59 # radial translation and phase rotation. Populate the nine
60 # remaining channels with this matrix.
61
62 -fill[args] ">
63 CPX=I;
64 orot=rot([0,0,1],deg2rad(CPX[1])); # phase rotation
65 xlat=eye(3);
66 xlat[2]=CPX[0]; # translation origin
67 [CPX[0,3,1],mul(orot,xlat,3)]; # -to-rim, i.e.
68 " # 'rotation & xlation'
69 # store above in
70 # 12-channel pixel
71 -permute[args] cyzx
72 -store[args] circles
73
74 # Screenspace transform.
75 foreach {
76 # Draw arabesques on the current image
77 # Designate it as the drawing "canvas".
78 -name. canvas
79 specw={int(min(w,h)/2)}
80 ssxfrm={"
81 sw=get('specw',0,0);
82 id=eye(3);
83 id[0]=sw;
84 id[2]=sw;
85 id[4]=-sw;
86 id[5]=sw;
87 id
88 "}
89 atk=0 # Accumulate "angular ticks"...
90 lastpt={vector3([0,0,1])}
91 firstpt={vector3([0,0,1])}
92 -repeat 3*$specw k=$> # Animation loop
93 # For each wheelie:
94 # increment by angular velocity
95 # find corresponding rotation matrix
96 # compose with radial argument image,
97 # compose with screenspace transform
98 # and plot via polygon().
99
100 -eval ">
101 const cc=$wcnt;
102 fpt=get('firstpt',3,0);
103 ik=get('k',0,0);
104 lpt=get('lastpt',3,0);
105 omega=get('atk',0,0);
106 sw=get('specw',0,0);
107 circs=get('circles',12*cc,0);
108 pp=vector3([0,0,1]);
109 imat=eye(3);
110 repeat(
111 cc,k,
112 idx=cc-k-1;
113 imat=mul(
114 mul(
115 rot([0,0,1],circs[12*idx+2]*omega),
116 circs[12*idx+3,9,1],
117 3
118 ),
119 imat,
120 3
121 );
122 );
123 ssx=get('ssxfrm',9,0);
124 plt=ssx*(imat*pp);
125 ik>0?
126 polygon(#$canvas,-2,[plt[0,2],lpt[0,2]],1,0xffffffff,255):
127 store('firstpt',plt,3,1,1,1);
128 store('lastpt',plt,3,1,1,1);
129 ik==(3*sw-1)?
130 polygon(#$canvas,-2,[fpt[0,2],plt[0,2]],1,0xffffffff,255)
131 "
132 atk={2*pi*($k/(3*$specw-1))}
133 -done #Animation loop
134 } #foreach
Annotations
Weeds, for those wishing to delve into them.
| Line | Remark |
| 21 | $=a A pseudo assignment. G'MIC transforms this into a series of actual assignments. This $-expression generates an assignment sequence with the base name a for however many command line items there may be. $a0 identifies the name of the script, so one could alter script behavior based on the script name. $a1… onward are the arguments. See Adding Custom Commands. There is nothing special about the base name a. It could be anything: $=fruitloops initializes command line variables $fruitloops0, …, $fruitloops<n>. See 42 for usage. |
| 25 | Argument Count: $# is an $-expression that resolves to the number of comma-separated arguments given to gtutor_wheelie. Thus, with the pseudo assignment shown in 21, the command line interpreter would resolve ${a{$#}} to the last command line argument. See also 42. |
| 25 | Argument Triplets: Wheelie specifications occur in groups of three, +r, ±θ and ±2πf, so modulo 3 inverted, !(($#)%3), resolves to True in such cases, enforcing arguments given three-at-a-time. Thus, the user employs triplets of successive arguments to specify wheelies, one triplet for each wheelie. Substitutions: $-expressions specifically appear in custom command definitions, such as the one of which we are in the midsts: gtutor_wheelie. See Adding Custom Commands. See also Substitution Rules for those substitutions that the command line parser recognizes in any setting, not just custom commands. |
| 32 | Math Expressions: Curly brace pairs here invoke the Mathematical Expression Parser. The present case sets the command line variable wcnt to the number of wheelies specified on the command line. $#, divided by three provides such, as each wheelie consists of three command line arguments. |
| 33-53 | Persistent Storage: Before Dynamic Arrays, it was not uncommon to harness images as persistent data storage, here image args (34), for mathematical environments as these do not persist. Data storage images also underlie Dynamic Arrays, but wrapped in a nice application programmer's interface (API). In this Old School approach, args is not intended for display but as an argument database, one to be shared across math expression invocations. Wheelie Database I: Each pixel in this "argument image" specifies aspects of one wheelie. Channels 0-2 hold +r, ±θ and ±2πf data, and this first repeat…done loop, 40-53, saves them for future reference; see 114-118. Channels 3-11 are reserved for the wheelie-specific affine transforms. To reduce computations in the animation loop between 92-133, we break the computation of the affine matrix into "stage 1" and "stage 2" phases. "Stage 1" precomputes matrices with only +r and ±θ items, which are time-independent. "Stage 2" computation occurs much more frequently, at every Δt tick, but with stage 1 computations done, there is only a need to composite an additional rotation into "stage 1", reflecting wheelie rotation during Δt. See 115. |
| 42 | Accessing Argument Lists: A pseudo assignment such as $=a, see 21, gives rise to a a number of actual command line variables $a0, $a1, …, $a<n>. An "array-like" addressing scheme may be carried out, which rad=${a{1+$j}} exemplifies. The curly-brace {1+$j} post-fixed to a is reminiscent of a decorator indexing the "j-plus-one" argument array item. However, suggestive though that notation may be, no actual array access is taking place — it is just syntax sugar. This sweetening relies on the kind of name coordination that the pseudo assignment $=a sets up: a set of variables with common basenames and numeric suffixes in progression. In fact, the command line interpreter undertakes a double substitution. The innermost braces ultimately invoke a mathematical expression; see 32. But before such, the command line interpreter looks up the current value of $j and substitutes it for the look-up value; then the mathematical expression parser is invoked. That tool "sees" just two literal numbers, 1 and the loop count which $j formerly referenced. The mathematical parser has no idea about $j; it exists in another universe. The mathematical parser has just two literal values; it adds these and hands the results back to the command line interpreter. The command line interpreter now regards the transformed construct anew: it is a variable ${a<n>} with <n> the number that $j represents. This engenders a second substitution, a look up for what $a, followed by some number <n>, represents. With foresight and planning, ${a<n>} actually exists, the look up of which rad duly acquires. So for those familiar with this syntax sugar, the process seemingly "accesses the argument array" and all goes well. However, should foresight or planning be lacking — misunderstanding the number of arguments, perhaps — then the look up proceeds anyway, likely returning the empty string of a command line variable used before it is assigned. From there, any number of subtle bugs may arise. Foresight and planning follows from a pseudo assignment such as $=a to set up the pseudo argument array. |
| 62-68 | Wheelie Database II: fill iterates over the args image, computing the "stage 1" affine transformations for each wheelie. Storage for each wheelie occupies one of the twelve channel pixels of the args image; In each step of the fill, the current arg image pixel, I, represents all that is known about one particular wheelie. |
| 63 | Pixel Accessors: Assigning I to CPX is not a (redundant) assignment of one vector to another, rather it is the creation of a vector from a pixel accessor function. The right hand side, I, is the pixel accessor; see Specific Functions, bullet points 5 – 10. There is a square-bracket form of the pixel accessor function; its signature, I[#_ind,offset,offset,_boundary_conditions], differs from the square-bracketed form applied to vectors: V[ <starting index>, <subvector length>, <step> ]. The aim here is to remap the pixel to the vector, CPX, so as to harness vector accessor function instead. See 67 following. This particular pixel accessor, I unadorned, lacks an explicit argument decorator, so the default is in play: I(#ind,x,y,z,interpolation,boundary_conditions) where x, y, and z are the predefined math expression variables that, under image iteration, assume the current image column, row and depth values. By default, pixel accessors reference the current image. An optional "hashtag-identifier" initial argument explicitly identifies an access source by an image list index or image name: #2 identifies the third image on the list, counting from the beginning (remember: zero-indexed: 0,1,2!); #-3 identifies the third image counting from the end of the list. #$bluishimag identifies the image named bluishimag, should one exist. If there is no image that is so named, or if any of the access identifiers reach beyond the extent of the image list, you cop yourself an access error. You can access in-between pixels. That is, pixel coordinates x, y and z may be reals with fractional parts — you access the void between pixels! What happens then? An interpolation takes place through one of three flavors: 0:nearest neighbor; the interpolator reports the value of the nearest pixel along each image axis; 1:linear; the interpolator reports the value taken from a linear ramp between the two actual neighboring pixels; 2:cubic; the interpolator reports the value taken from a cubic spline intersecting the two actual neighboring pixels. See Pixel Accessors: Kinds of interpolation. You can access off-image pixels; perhaps you have overidden x with a value far exceeding the image width. What happens then? You apply boundary policy via boundary conditions: 0:dirichlet, the off-pixel is black, 1:neumann, the off-pixel is the same as the nearest edge pixel, 2:periodic, images repeat out to infinity along all axes; the off-pixel assumes the value of wherever it is in this repeating cycle, or 3:mirror, edges are mirror axes where images flip, and flip again out to infinity; the off-pixel assumes the value of wherever it is in this mirror repeating cycle. See Images Have Edges: Now What? for the deep dive. Some pixel accessor functions use a square-bracket decorator, these intended to reference images as if they were one dimensional arrays: I[_#ind,offset,_boundary_conditions]. It is easy to confuse this notation with accessing items of a vector, also using square brackets, and, by extended confusion, taking I to be a vector. Don't confuse this square bracket flavored pixel accessor with vector accessors, described later; see 67. |
| 64 | Making Rotation Matrices: rot() generates pure rotational matrices: 2 × 2 for two dimensional work and 3 × 3 for three dimensional. In the latter form, one provides the axis of rotation to complete the specification: [0,0,1] identifies the three-space +z unit axis. That we are operating in three dimensions may give one reason to pause. Recall our preference for working with homogeneous points, inhabitants of a three dimensional projective space, so that we can encapsulate both rotation and translation in one transform — as well as disambiguating points from vectors. In this case, the axis of choice is the +z axis, perpendicular to the canvas, so that when we rotate points in the canvas plane, they stay in the canvas plane. The first use of this function gives us orot, origin rotation derived from θ, the second item of the wheelie vector. deg2rad() conveniently converts this item from degrees to radians. So does the ° operator — the degree symbol. Thus 45.739° in a G'MIC math expression quietly transforms itself into ≈ 0.798296 radians. Consult your operating system manual on how to obtain off-keyboard characters if you cannot find the ° symbol on it. |
| 65,67 | Wheelie Matrix Composition I: We generate the translation matrix, xlat by starting with the 3 × 3 identity matrix, as furnished by eye(). In an affine transform, matrix elements two and five embody spatial displacement. We set only an x displacement, this the length of the wheelie; what of y (xlat[5])? Recall from the main discussion that we view individual wheelies in a relative way, so it suits us to build up the local wheelie transform where the wheelie itself is in a standard orientation: zero degrees, aligned to the +x axis. Thus, in this local space, there is no displacement in y. |
| 67,68 | As noted before ( Wheelie Database I, 40-53), CPX just holds +r, ±θ and ±2πf; we assemble a new version of CPX, one that additionally contains the time-independent "stage 1" wheelie transform matrix; see Figure 2. We re-compose this new version from a 12 item vector composed of two fields. The first field, items 0 - 2, is a copy of the initial three fields of CPX and contains +r, ±θ and ±2πf, obtained during command line processing; see 40-55. The matrix multiplication mul(orot,xlat,3) populates the second field, items 3 – 11; mul() produces a vector9, the 3 × 3 "stage 1" wheelie transform. Wheelie Matrix Composition II: The second field composing the wheelie vector harnesses mul() to multiply together matrices orot, the rotation component generated from ±θ, and xlat the translation component generated from +r. The right-to-left multiplication, or composition, of the translation and rotation matrices produces the wheelie matrix, which transforms a point at the origin of the wheelie to its tip; it reflects the combined operation of displacing the point along the +x axis by distance +r, then rotating by ±θ. Matrix Multiplication: Order Matters: Care must be taken, for the right-to-left composition of a translation and a rotation is not the same as a left-to-right composition. With the latter, the resulting matrix reflects the combined operation of first rotating the point at the origin, and then translating it. Alas! The rotation of a zero-length position vector — a point — is of no consequence: a point rotating around itself remains unchanged. That leaves a translation without rotation, a less-than-full operation. That is why the composition starts with xlat, generating a positive length displacement vector aligned along +x, to which we compose orot, rotating that displacement vector around the local origin. The non-communicative quality of matrix algebra is a source of many an interesting bug — amusing after the fact, exasperating in the moment. |
| 67 | Vector Accessor Function: CPX[0,3,1] is an example of a vector accessor function, which extracts subvectors from source vectors. The present example copies +r, ±θ and ±2πf from CPX to the fill return vector. The accessor function's three arguments, [0,3,1], correspond to [ <starting index>, <subvector length>, <step> ]. The first argument marks the index in the source vector where the subvector starts. It is the only required argument and, used in isolation, simply extracts a single item from the source vector. The second argument, if present, sets the subvector's length. Thus V=[0,1,2,3,4,5,6,7,8,9]; SV=V[5,3] sets SV to [5,6,7], the three item subvector beginning at index = 5. The third argument, if present, sets the step, and defaults to increments of one item. Thus V=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15];V[0,4,4] retrieves the subvector [0,4,8,12], the four item subvector starting at index 0 in the source vector and consisting of every fourth item thereafter until a length of four items is obtained. A vector accessor function can only read vectors; it cannot write them. This precludes its use on the left hand side of an assignment. For that, consider copy(), which can transcribe a subvector from a source to a destination vector, or sequencing a new vector's content within a pair of square brackets, as done in line 67. |
| 67 | Implied Assignments: As the last statement in the math expression argument to fill, the re-composed vector12, [CPX[0,3,1],mul(orot,xlat,3)], undergoes an implicit vector-to-pixel conversion, updating the current "wheelie entry" in the database image args. |
| 71-72 | Passing Data to Math Expressions: Having filled the image-based "wheelie database", we harness store to make the wheelie data accessible to any ensuing math environments. These may do so through the circles image storage variable. The permutation prior to store reorganizes the args image; the new permutation leaves wheelie components arrayed along the arg image x axis instead of along its spectral axis and make for more straightforward access in the arabesque drawing loop, 92-133. |
| 74-88 | Screen space: We form another transformation matrix, xxsfrm, based on specw, a resolution metric. This matrix relates one unit of distance in the wheelie computation space to half of the smaller image dimension. This heuristic anchors computational measure to a definite number. The resolution metrix specw figures in a number of sizing tasks, such as scaling the number of plots necessary to draw an arabesque (92). Matrix xxsfrm flips the direction of the y axis and locates the plotting origin in the upper left hand corner, in keeping with pixel images. When all other transforms have been carried out on arabesque plots, xxsfrm situates the plot in a pixel image. See 123-124. |
| 92-133 | Animation Loop: The arabesque animation loop plots one mark of the arabesque per iteration. 92: -repeat 3*$sw k=$> … -done establishes the number of plots; k grows with larger images. The multiplier, 3, is another heuristic; lower this multiplier for faster, sparser plotting. |
| 110-122 | Integrated Matrix: The repeat() mathematical function carries out the pairwise aggregation of local matrices into an all-embracing translation from the root of the wheelie chain to its tip. On repeat()'s denouement, imat ( intergrated matrix ) embodies this across-the-board translation. This is the "…compounding (of) individual circular motions into wider localities" described in the text. The loop walks from tip to root, cc-k-1 ⇒ idx. For each wheelie, idx, in a chain with cc links, the loop -repeat cc,k, … first retrieves wheelie idx rotation rate, 2πf, via a vector access: circs[12*idx+2] (67). To ascertain wheelie idx rotation to the present, we multiply this rotation rate with accumulated time: omega, obtaining aggregate rotation 2πft. We need to embody this rotation in an affine space transform to compound it with the kindred transforms of antecedent wheelies. To this end, we harness rot() to generate a rotation matrix around the affine space +z axis. This pure rotation matrix embodies the time-dependent rotation of wheelie idx. The inner mul() operation, 114-118, composes this time-based rotation with the wheelie's time-independent displacement and orientation matrix, (+r, ±θ), pre-computed back in "stage 1" (67-68 Wheelie Matrix Composition II:), retrieved through circs[12*idx+3,9,1]. The composition of these time-dependent and -independent matrices turns out the dynamic local motion of wheelie idx. The outer mul() expression, spanning 113-121, rolls this local motion into imat. Dropping out of this repeat loop completes imat's composition, a grand finale matrix that embodies the entire transform of a point from the origin of the wheelie chain up to the tip of the final wheelie. |
| 123-134 | The bottom of the arabesque drawing loop concerns itself with plotting arabesque marks: line segments between adjacent Δt plots and drawn by polygon(). The drawing loop maintains a two-plot window, realized by storage variables firstpt and lastpt. These points are in display space, so the matrix responsible for that transform is summoned from storage variable ssxform. Recall 79-88. imat*pp carries the point pp from the origin to the wheelie tip. It is subsequently transformed by ssx into a display space plot. To create a two point plotting window, the drawing loop retains the plot of the previous iteration in lastpt and draws from that to the current plot; before the iteration finishes, the current plot becomes the next inhabitant of lastpt, to serve in a similar capacity in the next iteration. That accounts for most drawing activity, excepting the initial and final boundary cases. Nothing is plotted in the first iteration. Instead, the initial plot is stashed to both firstpt and lastpt. Through all remaining iterations, up to the last, firstpt is undisturbed. When the last iteration is realized and plotting has taken place, there remains a gap between firstpt and lastpt. These become plot points for an extra, final call to polygon(), which closes the gap between the initial and final plots, finishing the arabesque. |
| Nearest Neighbor | ![(255,18^236,134^170,215) =>. yeloblu 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,0) =>. yeloblunearneigh _parse_cli_images rs[yeloblu] 27.7%,,5 rs[yeloblunearneigh] 50%,,5](img/_255_18_236_134_170_215_yeloblu_16_1_1_3_I_yeloblu_x_w_1_0_0_0_yeloblunearneigh_parse_cli_images_rs_yeloblu_27_7_5_rs_yeloblunearneigh_50_5.png) |
| gmic \ -input (255,18^236,134^170,215) \ -name. yeloblu \ -input 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,0) \ -name. yeloblunearneigh | |
| Linear | ![(255,18^236,134^170,215) =>. yeloblu 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,1) =>. yeloblulinear _parse_cli_images rs[yeloblu] 27.7%,,5 rs[yeloblulinear] 50%,,5](img/_255_18_236_134_170_215_yeloblu_16_1_1_3_I_yeloblu_x_w_1_0_0_1_yeloblulinear_parse_cli_images_rs_yeloblu_27_7_5_rs_yeloblulinear_50_5.png) |
| gmic \ -input (255,18^236,134^170,215) \ -name. yeloblu \ -input 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,1) \ -name. yeloblulinear | |
| Cubic | ![(255,18^236,134^170,215) =>. yeloblu 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,2) =>. yeloblucubic _parse_cli_images rs[yeloblu] 27.7%,,5 rs[yeloblucubic] 50%,,5](img/_255_18_236_134_170_215_yeloblu_16_1_1_3_I_yeloblu_x_w_1_0_0_2_yeloblucubic_parse_cli_images_rs_yeloblu_27_7_5_rs_yeloblucubic_50_5.png) |
| gmic \ -input (255,18^236,134^170,215) \ -name. yeloblu \ -input 16,1,1,3,I(#$yeloblu,x/(w-1),0,0,2) \ -name. yeloblucubic |
With pixel accessor function I, sixteen samples are taken between the two pixels constituting yeloblu; these populate a sixteen pixel wide image. The three trials employ each interpolation schemes provided by I.
Interlude
So gtutor_wheelie plots arabesques. Maybe it can do better: meaning, maybe it can do faster. But there's no budget for faster. You're paid off, walking down the street, counting money — but thinking: 'Wheelie could be faster.'gtutor_wheelie inches-along-the-curve, each step passing just Lilliputian line-segments to polygon(). polygon() is mostly setting up and tearing down. Overhead weighs every step.
But everyone is happy — or, at least, nobody is unhappy. So there you are, thinking gtutor_wheelie can do better: meaning, Wheelie could be faster — should anyone care to spring for the bid…
Well. You rework it anyway. That pulls you into the Deep Dive.
| Next: | Deep Dive |
Updated: Sun 22-January-2023 22:22:58 UTC Commit: 846e5989e3a4


 Home
Home Download
Download News
News Mastodon
Mastodon Bluesky
Bluesky X
X Summary - 17 Years
Summary - 17 Years Summary - 16 Years
Summary - 16 Years Summary - 15 Years
Summary - 15 Years Summary - 13 Years
Summary - 13 Years Summary - 11 Years
Summary - 11 Years Summary - 10 Years
Summary - 10 Years Resources
Resources Technical Reference
Technical Reference Scripting Tutorial
Scripting Tutorial Video Tutorials
Video Tutorials Wiki Pages
Wiki Pages Image Gallery
Image Gallery Color Presets
Color Presets Using libgmic
Using libgmic G'MIC Online
G'MIC Online Community
Community Discussion Forum (Pixls.us)
Discussion Forum (Pixls.us) GimpChat
GimpChat IRC
IRC Report Issue
Report Issue