From Arabesques, Wheelies
| Wheelies | Interlude | Deep Dive | From Wheelies, Arabesques |
| From Arabesques, Wheelies | Wheelie Animations |
 12. An Unknown Arabesque | So much for putting things together. Now let's take things apart. Figure 12 is an arabesque about which we know little. We might suppose that some cardinal sum defines it — but that is a supposition. In truth, all that we have are plot points. Still, if we allow ourselves to suppose, then what might be the terms of the allied cardinal sum? The law of exponents provides a clue. From this law, the multiplication of two wheelies results in a new product wheelie rotating at the sum of its antecedents' rotational rates and oriented along those antecedents' combined bearings. The ensuing radius is the product of the antecedents' radii; see Equation 5. |

Should the two antecedents have equal rotational rates but different handedness (née signs), they compose a chiral pair and "annihilate" each other in useful ways. Under multiplication, their equal-but-opposite rotational rates cancel; their radii and initial orientations form a time-invariant phasor. Figure 13 illustrates the case:
| 13. Same rate. Opposite handedness. The wheelies collapse into a non-rotating phasor. |
| Chiral pairs, wheelies having like rotational rates but of different handedness, say, f₁ = 5 Hertz and f₂ = –5 Hertz, produce under multiplication time-invariant phasors. Under multiplication, the combined rotation rates of the two wheelies cancel; t vanishes; a "residue" phasor ensues. In this example, the phasor's modulus is one, the product of two unit length radii, and its angular argument is 60°, the sum of the two antecedents' orientations, 23° and 37°. |
This vanishing act provides the pith for an "analytical engine", one that picks out the terms of a cardinal sum. Here's the key: the product of two wheelies allows but two outcomes:
| 1. | Outcome One – Terms Not a Chiral Pair: The product wheelie has the same average position as its antecedents. This is so because the product wheelie rotates at some non-zero rate, even if it is vanishingly small — as small as we dare imagine and smaller! The product wheelies still trace circles over the infinite run: t ∈ (–∞ … ∞) and even if the trace takes millennia to complete, it scribes a circle when complete and that figure's average position lies on the origin, as with its antecedents. |
| 2. | Outcome Two – Terms Are a Chiral Pair: The product is a time-invariant — not rotating! — phasor. For any period t, the phasor is "stuck" — its offset displaces the resultant arabesque from the centers of gravity of its antecedents, raising the flag of wheelie anihilation. |
We may not know anything about how Figure 12 comes about — but we don't care. We care only about some collection of wheelies that emulates Figure 12. Such a collection serves as a model for the arabesque, and the "analytical engine's" job is to produce that model: a collection of wheelies that form a cardinal sum which we can "suppose" defines the arabesque. For all practical purposes it does — so long as the margin of error between the model we have derived and the plots we have been given is sufficiently small.
So let us suppose, by fiat, that the arabesque's plot points are an outcome of some supposed cardinal sum, one that we aim to model. We begin by multiplying these plot points by trial unit wheelies: r = 1, θ = 0° across a range of rotational rates f. We would expect, with each trial, occurrences of either Outcome One or Outcome Two, as if we were making trial multiplications with the supposed cardinal sum itself. That is, the product arabesque arising with each trial:
| 1. | has the same center of gravity as the antecedent arabesque: Outcome One prevails; the trial unit wheelie does not form a chrial pair with any terms of the supposed cardinal sum. |
| 2. | has an offset center of gravity from the given arabesque. Outcome Two prevails; the trial unit wheelie forms a chiral pair with a term of the supposed cardinal sum. |
In the second outcome, the center of gravity offset stems from a residue phasor of "anihilated" chiral pairs. In that case, the rotation rate of the trial unit wheelie is the same as that of a term of the supposed cardinal sum, but of opposite hand. We can suppose that there is only one such term allied with Outcome Two, for if there are others, such could be combined into a single aggregate, all having a common rotation rate.
With Outcome Two, we establish exactly one term of an approximating cardinal sum:
| 1. | The rate of rotation of the identified term, f, is that of the trial wheelie, but of opposite hand. |
| 2. | The orientation of the identified term, θ, is the sum of orientations of the identified term and the trial wheelie. Since the trial wheelie has an orientation of zero degrees, the sum of orientations θ is wholly that of the identified term. Its measure is the orientation of the residue phasor. |
| 3. | Similarly, the radial length of the identified term, r, is the product of radii of the trial unit wheelie and the identified term. Since the trial unit wheelie has a radius of one, the radial product equals the length of the identified term. The phasor's length, then, is r. |
And so it goes. We pick off supposed cardinal sum terms by multiplying data sets with trial wheelies drawn from a sufficiently wide frequency band, one somewhat narrower than f ∈ (–∞ … ∞) — which would take awhile to evaluate. Here are the particulars:
The "Analytical Engine"
| 1. | Choose a Nyquist Sampling Rate, N, "sufficiently large" to anticipate the fastest expected rotational rate f — an educated guess to prevent the engine from running forever. |
| 2. | Introduce a container of 2N complex numbers, S (for "spectrum"), initialized to zero. |
| 3. | Regard the arabesque under analysis, A, be the multiplicand data set for a series of trial multiplications with successive unit wheelie multipliers, exp(–i2πft) for f ∈ ( –N,…, N ). |
| 4. | For A and for each integer rotational rate f: |
| 5. | Evaluate the product A × exp(–i2πft) ⇒ A'. |
| We evaluate the unit wheelie, exp(–i2πft) over t ∈ [0 … 1] for as many samples as those comprising A. This provides the multiplier data set. The pairwise multiplication of the two data sets, multiplicand and multiplier, carries out A × exp(–i2πft) ⇒ A'. | |
| 5a. | Take the difference of the average position of A and A' ⇒ S[f]. |
| 5b. | Case 1. A' has a center of gravity unchanged from the multiplicand, A. S[f] = 0i. |
| 5b. | Case 2. A' has a center of gravity differing from the multiplicand, A. S[f] ≠ 0i. |
| 6. | If f < N, go to 4., otherwise go to 7. |
| 7. | The collection S contains a frequency domain spectrum, coefficients approximating the terms of a cardinal sum that we suppose defines arabesque A. |
| 14. The frequency domain spectrum has a circular topology. Pixel coordinates correspond to rotational rates — frequencies, and clockwise or counterclockwise handedness. Negative and positive coefficients populate pixels to the left (negative, clockwise) and right (positive, counterclockwise) of ω₀ and meet at the Nyquist Sampling Rate frequency, ωn. A pixel's complex value at a particular image coordinate encapsulates one term of a cardinal sum. The value itself captures the orientation, θ, in the argument of the complex number, and its magnitude, r, in the modulus. |
Here is the "analytical engine" in operation:
| 15. Annihilated Wheelies Kick the Center of Gravity |
| Phase Diagram | Presents successive A × exp(–i2πft) ⇒ A' as f ranges from –12 to 12 Hertz. The evaluation of A × exp(–i2πft) ⇒ A' pairwise multiplies the unit vectors comprising exp(–i2πft) with their counterparty A plots. This effects angular additions that circular-shift plots of A' from their counterparts A to an amount commensurate with t. The effect is to first wind A' counterclockwise around the origin, then clockwise. Observe that the plot associated with t=0 does not move. This notwithstanding, at a frequency of annihilation, chiral pairs vanish and "residue" complex numbers, an exemplar illustrated in Figure 13, offsets the average position of A' with respect to A, as indicated by the red dot. The offset is to a point on the complex plane equal to a partial of arabesque A. This offsetting of the product arabesque from the origin signals a chiral pair annihilation and the concomitant detection of a cardinal sum term. Ideally, the detection of such a term should occur at precisely one frequency. Instead, the red dot motion appears to have a "fuzz factor" in that it moves continuously around a solution, which is at some sort of maximum offset from the origin. This small calamity arises because it is not practical to evaluate f ∈ (–∞ … ∞). With the evaluation of necessarily finite frequency ranges, there will be vanishingly small frequencies arising from trials very close to the rotational rates of chiral pairs; these will have periods substantially longer than the one revolution duration of the product arabesque's drawing, and that gives rise to non-zero plot averages. These engender faux solutions that skew A' from the origin just as a true solution would, and their aggregate behavior gives rise to spectral domain notches centered on chiral pairs and admits a "red dot flutter", setting a definite resolution limit on discerning chiral pairs at very nearly identical frequencies. There is little to be done about this resolution limit. C'est la vie. |
| Time Domain | Draws the real and imaginary components of A' in the time domain as f ranges from –12 to 12 Hertz. The dotted vertical lines demark periods, each of duration 1/f, and indicates the number of times A' wraps around the origin. Notice that the stretching is very small on the left hand side, but large on the right, reflecting "radial stretching". |
| Frequency Domain | Tracks how S fills with coefficients. The tracking does not portray these as complex numbers; the frequency domain window displays their modulii but not their angular arguments. Limited as this may be, non-zero coefficients pop up at abscissae f ∈ {-5, -2, 1} Hertz. These are the frequency domain coordinates for the coefficients of the supposed cardinal sum that plots Figure 12. |
Here is a table of farthest extents from the origin of centers of gravity during the "analytical engine's" run:
| – Rectangular C.O.G. | Radial C.O.G. | Hertz |
| 0.358614 –0.109639j | 0.375 ∠ –17° | 1 |
| 0.358614 –0.109639j | 0.375 ∠ –17° | –2 |
| 0.222752 –0.113498j | 0.250 ∠ –27° | –5 |
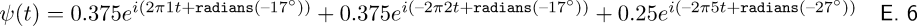
1 cexpsum:
2 size=255
3 # complex parameter ramp plotted on the
4 # imaginary axis.
5 -input 360,1,1,2,'[0,2*pi*x/(w-1)]'
6 -name. tau
7
8 # evaluate a wheelie-sum
9 -fill[tau] "0.375*cexp(I-[0,17°])+
10 0.375*cexp(-(2*I+[0,17°]))+
11 0.250*cexp(-(5*I+[0,27°]))"
12
13 # transform arabesque plots to a canvas
14 # drawing surface.
15 -fill[tau] "begin(
16 sw=get('size');
17 id=eye(3);
18 id[0]=sw;
19 id[2]=sw;
20 id[4]=-sw;
21 id[5]=sw
22 );
23 (id*[I(x,y),1])[0,2]
24 "
25 # paint the arabesque plot points on a
26 # canvas: white on black.
27 -permute[tau] cyzx
28 -input {2*$size},{2*$size},1,1
29 -name. canvas
30 -eval "PV=crop(#$tau);
31 polygon(#$canvas,
32 -int(size(PV)/2),
33 PV,
34 1,
35 0xffffffff,
36 255
37 )"
38 -output[canvas] unknownarabseque.png
2 size=255
3 # complex parameter ramp plotted on the
4 # imaginary axis.
5 -input 360,1,1,2,'[0,2*pi*x/(w-1)]'
6 -name. tau
7
8 # evaluate a wheelie-sum
9 -fill[tau] "0.375*cexp(I-[0,17°])+
10 0.375*cexp(-(2*I+[0,17°]))+
11 0.250*cexp(-(5*I+[0,27°]))"
12
13 # transform arabesque plots to a canvas
14 # drawing surface.
15 -fill[tau] "begin(
16 sw=get('size');
17 id=eye(3);
18 id[0]=sw;
19 id[2]=sw;
20 id[4]=-sw;
21 id[5]=sw
22 );
23 (id*[I(x,y),1])[0,2]
24 "
25 # paint the arabesque plot points on a
26 # canvas: white on black.
27 -permute[tau] cyzx
28 -input {2*$size},{2*$size},1,1
29 -name. canvas
30 -eval "PV=crop(#$tau);
31 polygon(#$canvas,
32 -int(size(PV)/2),
33 PV,
34 1,
35 0xffffffff,
36 255
37 )"
38 -output[canvas] unknownarabseque.png
unknownarabesque.png, you will find, reproduces Figure 12 in glorious, bi-valued black-and-white.
Or, if we want to create a chain of delta wheelies that also draws the arabesque, we may pair-wise difference the terms of Equation 6, say, in just the order of terms presented in that equation:
| Term | +r, ±θ | ±f | Δθ, Δf |
| 1. | 0.375 ∠ –17° (343°) | 1 Hertz | Root |
| 2. | 0.375 ∠ 0° | –3 Hertz | Δθ=–17°–(–17°), Δf=–2–1 |
| 3. | 0.250 ∠ –10° (350°) | –3 Hertz | Δθ=–27°–(–17°), Δf=–5–(–2) |
and then give it a whirl:
randomclover:
-command scripts/wheelie_simple.gmic
-input 512,512,1,1
-name. canvas
-gtutor_wheelie[canvas] 0.375,-17,1,0.375,0,-3,0.25,-10,-3
-name. wheelie
# White on black arabesque
-output[wheelie] plain.png
# Tiled and randomly colored arabesque
-dilate[wheelie] 8
-label[wheelie] 3
-input 1,10,1,3,'u([255,255,255])'
-name. palette
-map[wheelie] [palette]
-remove[palette]
-gtutor_tileit[wheelie] 0,0.25,1,1,1,0,8,1
-name. tiled
-output[tiled] clover_figure-14.png
-command scripts/wheelie_simple.gmic
-input 512,512,1,1
-name. canvas
-gtutor_wheelie[canvas] 0.375,-17,1,0.375,0,-3,0.25,-10,-3
-name. wheelie
# White on black arabesque
-output[wheelie] plain.png
# Tiled and randomly colored arabesque
-dilate[wheelie] 8
-label[wheelie] 3
-input 1,10,1,3,'u([255,255,255])'
-name. palette
-map[wheelie] [palette]
-remove[palette]
-gtutor_tileit[wheelie] 0,0.25,1,1,1,0,8,1
-name. tiled
-output[tiled] clover_figure-14.png
 |
| 16 Arabesque Dressed in Tiles |
No doubt, there are some of you out there — in moods admonitory — who would chastise us for our frivolity.
Aye. We could have applied the tilings and baubles and glitz direct to Figure 12, already in hand, instead of fetching one anew by some bonzer Rube Goldberg apparatus — just the sort of superfluity that one might expect from a New York City civil servant.
But — Phht! — does not any poetic sense — any sense of splendor — grace your jaded souls? Have you no inclinations to set off for nameless vales, cross hither into some hidden hollow, nestled darkly by an uncharted stream, and delight in countless unscored trills of bird song?
There are things tenanting caves deep in yonder hills that fit no recorded taxonomy, and yet — here in the mysteries there are guises that strike some as familiar. This analytic engine, for instance, is not of our authorship. It first turned its trick in 1822, with Jean-Baptiste Joseph Fourier's Théorie analytique de la chaleur ( "The Analytical Theory of Heat" ). It is the well known — celebrated, even — Discrete Time Fourier Transform. The collection S, its product (whimsically) comprised of annihilated chiral remnants, is more properly a Fourier series representation of arabesque A:
![\begin{matrix} S_N(t) = \displaystyle\sum_{f = –N}^{N} c_{f} \cdot e^{i(2\pi f t + \psi_{f})} & t \in [0,\dots ,1] & \textsf{E. 7} \end{matrix}](img/_begin_matrix_S_N_t_displaystyle_sum_f_342_200_223N_N_c_f_cdot_e_i_2_pi_f_t_psi_f_t_in_0_dots_1_textsf_E_7_end_matrix_.png)
Equation 7 almost looks like a cardinal sum. The terms' coefficients are complex, not scalar radii. But a notational rearragement can span that gap:

With this rewritten template, we arrive at the "cardinal sum" representation of Equation 7.
On the whole, G'MIC embodies From Arabesques, Wheelies in its fft command. The Analytical Engine's reduction of arabesques to elemental wheelies parallels that of a Fourier Series reduction of periodic signals to so many sinusoids. -fft is the "analyzer" that fractionates the whole into parts. Given the arabesque, it lays bare the constituent wheelies.
Conversely, ifft encompasses From Wheelies, Arabesques. It regards a collection of wheelies as so many "spectral basis functions" from which we synthesize spatial signals. Indeed, -ifft is the "synthesizer" that composes collections S, complex r ∠ θ in a frequency domain spectrum, into analogous time series.
Armed with these spectral/spatial analytical and synthesizing functions, let's rewrite gtutor_wheelie with the following aims:
| 1. | Make a spectral implementation based on the complementary operations fft and ifft. Arabesques are spatial analogs of a spectral sampling. |
| 2. | Separate concerns: split the implementation into interpretive and rendering commands. Make a wrapper to emulate the original gtutor_wheelie. |
| 3. | Optimize our use of polygon(); give it all plot points in one swell foop. |
Such ambitions gives rise to a revised wheelie_simple.gmic, called spectralarabesque.gmic:
( Download spectralarabesque.gmic ):
spectralarabesque.gmic
1 #@cli gtutor_fwheelie : radius₀,orientation₀,angular_velocity₀…
2 #@cli: Compose an arabesque from a chain of delta wheelies, a
3 #@cli: series of triplets, each consisting of a radial
4 #@cli: (+float), orientation (±degrees, float) and rotational
5 #@cli: rate (±integer) data. Draw the corresponding arabesque
6 #@cli: on the selected images.
7 #@cli: $
8 gtutor_fwheelie : -check "!(($#)%3)"
9
10 -foreach {
11 specw={int(min(w,h)/2)}
12 -gtutor_mkspectral $specw,$*
13 -gtutor_specplot[0] [-1]
14 -remove[-1]
15 }
16
17 #@cli gtutor_mkspectral : spec_w,rad₀,orient₀,ang_velocity₀…
18 #@cli: Generate a two channel discrete frequency domain image
19 #@cli: corresponding to the supplied delta wheelie parameters:
20 #@cli: +r, ±θ and ±f on the command line, one triplet for each
21 #@cli: delta wheelie. Image suitable as a gtutor_specplot
22 #@cli: selection, which draws the arabesque.
23 #@cli: $
24 gtutor_mkspectral: -check "isint(${1}) && ${1}>0 && !(($#-1)%3)"
25
26 # Expect spectral width followed by data triplets $a1,$a2,$a3…
27 dwheelcnt={($#-1)/3}
28 specw=$1
29 -input 3,1,1,$dwheelcnt,${2--1}
30 -name[-1] args
31 -store[args] deltawheelies
32
33 #coeffcient image: 'carray'
34 -input $specw,1,1,2
35 -name[-1] carray
36 -store[carray] coefficientarray
37
38 # Find canonical sum by aggregating delta wheelies.
39 # Insert terms into spectral image using rotation
40 # rate as spectral coordinates.
41 # Σf -> $accsf; Σθ → $acca
42 -eval "const wc=$dwheelcnt;
43 const sw=$specw;
44 dw=get('deltawheelies',wc*3);
45 ca=get('coefficientarray',sw*2);
46 acca=0;
47 accsf=0;
48 repeat(wc,k,
49 r=dw[3*k];
50 acca+=deg2rad(dw[3*k+1]);
51 accsf+=dw[3*k+2];
52 aidx=accsf%sw;
53 ca[aidx]+=r*cos(acca);
54 ca[sw+aidx]+=r*sin(acca);
55 );
56 store('coefficientarray',ca,sw,1,1,2)"
57
58 # carray: frequency domain image generated
59 # from the given delta wheelie chain.
60 -input $coefficientarray
61 -name. carray
62
63 # Scale freq. domain by domain length.
64 -mul[carray] $specw
65
66 #@cli gtutor_specplot : [spectrum]
67 #@cli: Generate an arabesque on selected images from
68 #@cli: the given argument: a frequency domain spectrum image.
69 #@cli: $
70 gtutor_specplot : -is_image_arg $1 gotimg=${} -check "$#==1 && $gotimg"
71
72 -pass$1 0
73 -name[-1] carray
74 # Frequency domain → time domain
75 -split[-1] c
76 -ifft[-2,-1]
77 -append[-2,-1] c
78 -name. temporal
79 -foreach[^temporal] {
80 -pass[temporal] 0
81 sw={min(w#-2,h#-2)}
82
83 # Screenspace transform.
84 -fill[temporal] ">
85 begin(
86 specw=$sw/2;
87 id=eye(3);
88 id[0]=specw;
89 id[2]=specw;
90 id[4]=-specw;
91 id[5]=specw;
92 );
93 (id*[I(x,y),1])[0,2];
94 "
95 -permute[temporal] cyzx
96 -eval "PV=crop(#$temporal);
97 polygon(#-2,
98 -int(size(PV)/2),
99 PV,
100 1,
101 0xffffffff,
102 255
103 )
104 "
105 -keep[-2]
106 } #foreach[^temporal]
107 -remove[temporal]
2 #@cli: Compose an arabesque from a chain of delta wheelies, a
3 #@cli: series of triplets, each consisting of a radial
4 #@cli: (+float), orientation (±degrees, float) and rotational
5 #@cli: rate (±integer) data. Draw the corresponding arabesque
6 #@cli: on the selected images.
7 #@cli: $
8 gtutor_fwheelie : -check "!(($#)%3)"
9
10 -foreach {
11 specw={int(min(w,h)/2)}
12 -gtutor_mkspectral $specw,$*
13 -gtutor_specplot[0] [-1]
14 -remove[-1]
15 }
16
17 #@cli gtutor_mkspectral : spec_w,rad₀,orient₀,ang_velocity₀…
18 #@cli: Generate a two channel discrete frequency domain image
19 #@cli: corresponding to the supplied delta wheelie parameters:
20 #@cli: +r, ±θ and ±f on the command line, one triplet for each
21 #@cli: delta wheelie. Image suitable as a gtutor_specplot
22 #@cli: selection, which draws the arabesque.
23 #@cli: $
24 gtutor_mkspectral: -check "isint(${1}) && ${1}>0 && !(($#-1)%3)"
25
26 # Expect spectral width followed by data triplets $a1,$a2,$a3…
27 dwheelcnt={($#-1)/3}
28 specw=$1
29 -input 3,1,1,$dwheelcnt,${2--1}
30 -name[-1] args
31 -store[args] deltawheelies
32
33 #coeffcient image: 'carray'
34 -input $specw,1,1,2
35 -name[-1] carray
36 -store[carray] coefficientarray
37
38 # Find canonical sum by aggregating delta wheelies.
39 # Insert terms into spectral image using rotation
40 # rate as spectral coordinates.
41 # Σf -> $accsf; Σθ → $acca
42 -eval "const wc=$dwheelcnt;
43 const sw=$specw;
44 dw=get('deltawheelies',wc*3);
45 ca=get('coefficientarray',sw*2);
46 acca=0;
47 accsf=0;
48 repeat(wc,k,
49 r=dw[3*k];
50 acca+=deg2rad(dw[3*k+1]);
51 accsf+=dw[3*k+2];
52 aidx=accsf%sw;
53 ca[aidx]+=r*cos(acca);
54 ca[sw+aidx]+=r*sin(acca);
55 );
56 store('coefficientarray',ca,sw,1,1,2)"
57
58 # carray: frequency domain image generated
59 # from the given delta wheelie chain.
60 -input $coefficientarray
61 -name. carray
62
63 # Scale freq. domain by domain length.
64 -mul[carray] $specw
65
66 #@cli gtutor_specplot : [spectrum]
67 #@cli: Generate an arabesque on selected images from
68 #@cli: the given argument: a frequency domain spectrum image.
69 #@cli: $
70 gtutor_specplot : -is_image_arg $1 gotimg=${} -check "$#==1 && $gotimg"
71
72 -pass$1 0
73 -name[-1] carray
74 # Frequency domain → time domain
75 -split[-1] c
76 -ifft[-2,-1]
77 -append[-2,-1] c
78 -name. temporal
79 -foreach[^temporal] {
80 -pass[temporal] 0
81 sw={min(w#-2,h#-2)}
82
83 # Screenspace transform.
84 -fill[temporal] ">
85 begin(
86 specw=$sw/2;
87 id=eye(3);
88 id[0]=specw;
89 id[2]=specw;
90 id[4]=-specw;
91 id[5]=specw;
92 );
93 (id*[I(x,y),1])[0,2];
94 "
95 -permute[temporal] cyzx
96 -eval "PV=crop(#$temporal);
97 polygon(#-2,
98 -int(size(PV)/2),
99 PV,
100 1,
101 0xffffffff,
102 255
103 )
104 "
105 -keep[-2]
106 } #foreach[^temporal]
107 -remove[temporal]
Spectral Annotations
Weeds, for those close to the ground.
| With a separation of concerns, gtutor_fwheelie reduces to a command that does little on its own; it is a wrapper that calls others to do what the old gtutor_wheelie did monolithically. Kudos to monolithia, perhaps, it's the one thing to do it all. But then, there's this: The old gtutor_wheelie renders a four delta wheelie chain on a 4096 × 4096 pixel image in about 2.3 ~ 2.5 seconds, its spectrally enhanced successor, gtutor_fwheelie, does the same throw in just 0.7 ~ 0.8 seconds — both times on a Xeon E5-2630, running at 2.2 GHz. So, performance has improved — we like performance! — but there's a Separation of Concerns benefit in the offing too. The monolithic gtutor_wheelie couldn't be picked apart. That sealed two useful functions within: (1) Determining the cardinal sum from delta wheelies, and (2) Rendering a cardinal sum's affiliated arabesque. With a dash or two of Separation of Concerns, these two functions emerge as distinct G'MIC commands. Now, with gtutor_mkspectral we can produce the spectral image itself without it being automagically turned into an arabesque — perhaps we have some further frequency domain manipulations in mind. And, with gtutor_specplot, we may obtain spectral images from other sources — not just wheelie chains — and render those as arabesques. | |
| Line | Remark |
| 8-15 | Wrapper: gtutor_fwheelie is a wrapper around gtutor_mkspectral, which finds the cardinal sum affiliated with a given chain of delta wheelies, and gtutor_specplot, which, given a spectral image argument, renders the affiliated arabesque. The remit charged to just gtutor_fwheelie is small: iterate over the selected images, if any, and for each, (a) determine its "spectral width," (b) generate a cardinal sum via gtutor_mkspectral and (c) render it via gtutor_specplot. The "cardinal sum" which gtutor_mkspectral generates takes the form of a frequency domain spectral image, a 1 × 2N, two-channel (real and imaginary), depiction of the discrete (integral) frequecy domain; see Figure 14. Note how gtutor_mkspectral's arguments have been formed. Command line variables naturally concatenate: $specw, , and $* together form one string, a comma-separated argument list. The latter, $*, is an $-expression for the argument list in the current scope. Essentially, gtutor_fwheelie is passing the arguments it has been given (these in $*) to gtutor_mkspectral, which will actually make use of them. This is in conjuction with the "spectral width" variable $specw, which gtutor_fwheelie assays from the current image. Once gtutor_specplot draws the arabesque, gtutor_fwheelie discards the cardinal sum, leaving only the image of the affiliated arabesque on the image list. |
| 24-65 | Cardinal Sum Tool: gtutor_mkspectral interprets the second and subsequent items of its argument list as delta wheelie triplets (+r, ±θ, ±2πf) and computes the terms of its affiliated cardinal sum, leaving this in the form of a spectral image on the image list. The command gtutor_mkspectral follows the algorithm accompanying Figure 9. It sizes the length of the spectral image per $specw, aka the spectral width, in pixels. See 64-68 The Spectral Image: for more on this sizing operation. |
| 29-30 | Fast Database: Compare lines 29-30 here, with the gtutor_wheelie functional counterpart. The aim in both places is to create a "delta wheelie database" from a command line sequence of arguments. The approach taken with gtutor_wheelie entails walking down the pixels of a "wheelie database image", one pixel for each delta wheelie. For a particular pixel, aka a "delta wheelie", the approach takes a block of three successive command line arguments, these r, θ, and 2πf delta wheelie constituents, and explicitly set-ing the pixel channels with these: r ⇒ channel R, θ ⇒ channel G and 2πf ⇒ channel B. It is, on the whole, a thirteen line exercise in pixel twiddling, but it does a yeoman job of transferring command line items to the "wheelie database." We won't be getting any Turing Awards with this but we got what we wanted. That said, line 29 performs the same set-up in just one line. We just flow pixels into the image in one atomic action. Recall that input operates with character streams as well as image files; the argument list ${2--1} is such an character stream. With this technique, G'MIC maps images to linear memory in row-major order; it is such that a fill of contiguous memory bytes runs first along the image's x axis and, only as rows fills, along the y. Further, an image's first x × y plane, channel 0 ( R ), fills before channel 1 ( G ). Finally all channels of an image's first slice, x × y × c, fills before the second slice. So, in this setting, we regard the argument list ${2--1} as an "character stream," which incorporates the argument list into the wheelie database in one fell swoop. No pixel twiddling needed. |
| 31-36 | Passing Data to Math Expressions: The heart of gtutor_mkspectral is an implementation of the cardinal sum algorithm, a G'MIC math expression given as an argument to eval and spanning lines 42-56. The procedure takes a chain of delta wheelies that we have composed into a "delta wheelie database," ordered from the chain's root to the tip. To make this data available to the math expression, we place it in a named command line variable, deltawheelies via the store command, 44. Similarly, we create a coefficientarray spectral image, 45, that the same math expression populates with spectral image data. These exemplify exchanging data sets with one or more G'MIC math expressions. |
| 38-58 | Delta Wheelies to Cardinal Sums: The plain language procedure to find the cardinal sum from an affiliated chain of delta wheelies accompanies Figure 9 in From Wheelies, Arabesques. It is realized here in this math expression argument of an eval command: accumulators Σf → $accsf; Σθ → $acca keep running totals of rotation rates and orientations. With each step of the walk along the chain, the running totals absorb another delta wheelie; the new accumulations provide another term of the cardinal sum. As these terms of the cardinal sum are bought forth they are plotted in the coefficient array. the accumulated rotation rate, modulo the spectral width, furnishes an index into the coefficient array. Note that the coefficient array, ca, lays the channels of the spectral image end-to-end, akin to a channel split, such that the trigonometric cosine and sine components are offset in ca by the spectral width stride, sw. With the iteration over the given delta wheelies complete, ca becomes suitable input to ifft, once converted from a math expression vector and back into an image. Such takes place through store, see 56, and input, see 60. |
| 60-64 | The Spectral Image: gtutor_mkspectral completes its construction of the spectral image by retrieving it from $coefficientarray and scaling it by the given spectral width. What is "spectral_width"? And why scale by it? gtutor_mkspectral emulates the behavior of of fft operating on a one dimensional set of spatially ordered plot samples. The number of samples — here, the "spectral width" — constitutes an abstract distance, the period length of the sample set on an infinitely long spatial axis. When it generates the spectral image, -fft scales the data in this sample set by the spectral width, encoding it in the set. But in carrying out this -fft emulation, gtutor_mkspectral has no idea what the spectral width is, so it must be told. The first argument given to gtutor_mkspectral is such a fiat declaration of spectral width. Strictly speaking, such a declaration is divorced from any particular reality; it becomes a convenient scaling factor, which can be harnessed in the interest of Art. |
| 66-107 | Spectral Plotting: In the revised scheme of gtutor_wheelie → gtutor_fwheelie, the spectral image plotter, gtutor_specplot changes in two ways: (a) it acquires a command line interface, and (b) it plots an entire arabesque data set of plot points in one throw; gone is the tedium of maintaining a Δt "plotting window," through which single line segments are fed to polygon() a pair-of-points at a time. The basis of this efficiency is the spectral → spatial transform performed by ifft which serves up the entire arabesque plotting data set in one transform. This is the pay-off from (a) first taking a Deep Dive, (b) establishing the relationship between delta wheelies and cardinal sums, and (c) uncovering the essential relationship between arabesques and cardinal sums: they are two sides of the discrete Fourier transform, and fft and ifft transforms our data to and from these spectral and spatial realms. |
| 72-80 | Passing Images Through Scopes: gtutor_specplot takes an image argument and draws arabesques on its selection set, however many images there may be in that set. It takes the spectral image as an image argument; pass facilitates the reading of image arguments from the command line. In the wild, -pass is almost always concatenated with a command line argument, here $1. which should resolve to an <open-square-bracket><image selection><close-square-bracket> string. The command is_image_arg checks that the argument accommodates that form. As G'MIC transforms its raw command line item list into a meaningful set of commands, and then enters the processing scope of that command, notation like pass$1 transforms to something like pass[1]. A built-in command, -pass then copies the selected images in the called context to the current, gtutor_specplot, context, incorporating the now-passed-images into the current scope's image list. This passing of images is necessary because, on the whole, the context of called G'MIC commands are more-or-less isolated from calling contexts. And while context passage commonly takes place with command invocation, it can also happen with loop iteration commands like foreach, which maintains its own, private image list, and which defaults to holding only the current image in the iteration for processing. A second use of the pass command appears at 84 to copy the temporal image into the private foreach image list. |
| 72-80 | Spectral to Spatial: With the spectral image in hand, it becomes a temporal data set via ifft; see 80. That is, the discrete Inverse Fourier transform brings the spectral image, populated with cardinal sum coefficients, into a time series — positions varying as functions of time. When plotted on an x × y plane, this time series looks like the arabesque. There remains mundane matters of scaling the series to the particular dimensions of selected images, each of which will have the same arabesque plotted on it, and scaled to the image at hand. We generate the temporal data set but once, and, within the foreach loop, rescale as needed. |
| 83-112 | foreach: Drawing the Arabesque: Drawing the arabesque borrows from the approach first advanced in rendering a cardinal sum. The foreach{…} iteration is an arabesque stamping machine. For however many images there are in the gtutor_specplot selection, this iterator sizes and stamps the arabesque on each member image in the selection. To achieve that, the iterator derives an affine transform matrix to project the arabesque onto the image, scaling it to fit in a square sized to the smallest dimension of the image, the minimum of either the image's width or height. See 85. With each iteration, the pass command furnishes a local copy of the arabesque plot points, these held in the image named "temporal." A math expression embodied in a fill command iterates over the plot points and scales each by the affine transform. Within the math expression, a begin(…) statement sets up that affine transform: id; 89-96. Recall that begin(…) statement blocks establish a set of commands that run once prior to the fill command's iteration loop. The remaining step, performed outside the begin(…) block, replaces each pixel with a transformed plot point, this through a pair of Pixel Accessors. See the Pixel Accessors article. The inner accessor retrieves the untransformed plot point. Once retrieved, the x and y plot points are recomposed into a homogeneous form with a third "pseudo" z = 1, coordinate so that it may be operated on by affine transforms. We scale and translate this homogeneous plot point by the affine transform id. Finally, we apply an "outer" accessor to the transformed three-vector homogeneous plot point, this for retrieving just the first two transformed coordinates, x' and y'; 97. The outcome of the second pixel accessor is the transformed two-vector plot point. Since this two-vector constitutes the last statement in the math expression, an implicit vector → pixel conversion and assignment takes place; the transformed coordinates now occupy what had been, heretofore, the original plot point. 99: We permute the plot points to align x' and y' along the spectral (channel) axis, a reorganization prompted by polygon(). 99-109 We graph all arabesque plot points in one polygon() call. These plot points reside in image temporal; the math expression function crop() introduces images into math expression environments, producing a vector from pixel data. Without dimensional arguments, crop(…) converts the entire image into a vector and assigns it to the left hand side element. Here, PV receives the vectorized plot points from crop(…). In turn, polygon(…) projects these onto the drawing image, the second from the end of the image list (#-2). The second argument represents a count of line segments: -int(size(PV)/2). The negative sign has been overloaded for this argument: signalling here: "plot the shape outline"; its absence signals "fill the shape". The third argument specifies the source of plotting data; the fourth parameter, 1 sets the opacity of the plotted image, here, fully opaque, zero signalling full transparency and fractional values k ∈ (0…1) some degree of partial transparency. A 32 bit hexadecimal, the fifth argument, specifies whether thirty two plot point sequences, starting at the beginning of the plotting pattern, are to be turned on or off, this for emulating line dot-and-dash patterns. Finally, the sixth and last parameter is a color vector; its length must match the channel depth of the image serving as a canvas. |
| Previous: | From Wheelies, Arabesques | Next: | Wheelie Animations |
Updated: Sun 22-January-2023 22:22:58 UTC Commit: 846e5989e3a4


 Home
Home Download
Download News
News Mastodon
Mastodon Bluesky
Bluesky X
X Summary - 17 Years
Summary - 17 Years Summary - 16 Years
Summary - 16 Years Summary - 15 Years
Summary - 15 Years Summary - 13 Years
Summary - 13 Years Summary - 11 Years
Summary - 11 Years Summary - 10 Years
Summary - 10 Years Resources
Resources Technical Reference
Technical Reference Scripting Tutorial
Scripting Tutorial Video Tutorials
Video Tutorials Wiki Pages
Wiki Pages Image Gallery
Image Gallery Color Presets
Color Presets Using libgmic
Using libgmic G'MIC Online
G'MIC Online Community
Community Discussion Forum (Pixls.us)
Discussion Forum (Pixls.us) GimpChat
GimpChat IRC
IRC Report Issue
Report Issue