A Full-Featured Open-Source Framework for Image Processing

Eigenvalues and Eigenvectors

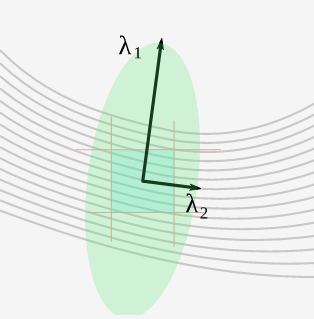Here's the bit about EigenOne and EigenTwo. They hold eigenvalues. So what are eigenvalues?

Eigenvalues tell us how large eigenvectors are.

Uh.

OK. Some of you seem to have pained expressions on your faces. You think maybe the discussion is going circular and the tracks we're following belong to us. Hang on.

Recall that we have unwired smooth from its usual connections, the pieces of G'MIC that figure out how to do anisotropic smoothing. Let's look at that anisotropic smoothing problem a little bit. Those pieces ultimately have to tell smooth what to do, and the medium of exchange is a tensor field. So if we study how the anisotropic smoothing bits go about setting up tensor fields, we'll garner insights on how to set up our own. Some of you with a bit of math background might want to look ahead to Eigen Thingys.

The anisotropic pieces of G'MIC which ultimately harness smooth look for edges. They want smooth to smooth around edges but not smooth over edges. That means they have to find edges.

What do edges look like to G'MIC?

They look like a couple of vectors. These point at right angles to one another.

One vector is called the gradient vector. It points along the steepest part of a gradient - a change of image intensity – in the vicinity of a pixel. The other is called the contour vector. It points at right angles to the gradient vector. When the gradient vector is big and the contour vector is small, then that looks like an edge to G'MIC. Otherwise ― “eh”.

So the smoothing bits look at the difference between EigenOne and EigenTwo, then at Cosine and Sine to see where the gradient is running. The direction in which smoothing needs to go runs at right angles to the gradient, its magnitude a function of EigenOne, EigenTwo, plus command line parameters. Look at diffusiontensors for details.

So here's the takeaway:

1.	EigenOne:	Holds the magnitude of the gradient vector. This is often represented by the symbol λ1. It runs from zero up to positive infinity, but we like to cap it at one. It's the eigenvalue associated with the gradient vector, but please don't talk to your dog that way; you'll just give the poor creature headaches.
2.	EigenTwo:	Holds the magnitude of the contour vector. This is often represented by the symbol λ2. It too runs from zero up to positive infinity, but we like to cap it at one. It's the eigenvalue associated with the – you guessed it! – contour vector. Ditto on the canine cautionary.
3.	Cosine:	The cosine of the angle along which the gradient vector runs. We only have to worry about 0° to 180° (0 … π) so the cosine run from -1 to 1.
4.	Sine:	The sine of the angle along which the gradient vector runs. Again, half the angular range so the sine runs from 0 to 1.

The eigen2tensor command expects these four gray scale images to be packaged into a pair of two-channel images, and it turns out a three channel field of tensors, and we're going to leave matters at that. Those feeling brave can dig into Eigen Thingys.

For now, it suffices to think of a tensor field as a set of instructions for smooth. One tensor for each pixel tells smooth how to blur in that locale. Here's its remit.

1.	Together, Cosine and Sine tell smooth the orientation of the gradient vector.
2.	EigenOne tells smooth how hard to blur along the gradient vector.
3.	EigenTwo tells smooth how hard to blur transverse to the gradient vector.

With these points in mind, Let's return to what happen when we ran EigenTwo from zero to one while EigenOne ran from one to zero.

1.	Cosine is a gray scale image with constant value zero, while Sine is constant value one, so the gradient vector at every pixel points straight up at 90°.
2.	Close to the top of the image, the EigenOne ramp is nearly one. That instructs smooth to blur hard along the gradient. Concomitantly, The EigenTwo ramp is nearly zero, telling smooth to blur only a tiny bit transverse to the gradient. Net effect: strong vertical blurring; minimal horizontal blurring. Obviously, at the bottom of the image, the situation reverses and smooth mainly blurs from left-to-right, transverse to the gradient, instead of up-and-down, along the gradient.
3.	In the middle of the image, EigenOne and EigenTwo are about equal, so smooth blurs as much one way as the other – a circular blur.

So:

1.	EigenOne, together with EigenTwo, combine to set the eccentricity of the blurring elipse.
2.	The amount of blurring is no more than the larger of EigenOne or EigenTwo.
3.	The direction is controlled by Cosine and Sine.

As a corollary, when EigenOne and EigenTwo are equal, the eccentricity is zero and the blur is circular. In this case, it hardly matters what angle Cosine and Sine reference as a circle has the remarkable property of looking the same no matter how it's turned. That's just the way they built this particular Universe. Our convention is to set Cosine to one and Sine to zero, corresponding to zero degrees.

And these, dear hearts, are the keys to Emerald City. We could close up shop right here and let you go off on your own. You can do whatever you want with these four gray scale images and -smooth will follow obediently along. Just observe the normalization limits. EigenOne, EigenTwo and Sine run from zero to one, Cosine runs from negative to positive one.

But you probably wouldn't mind a few more examples. Yep. We thought so. See you on the next page.

---