Riffs
 Leonard Raven-Hill: 'For Auld Lang Syne' | Riffs and finger exercises — how do you do them? Two ways: 1. Use the run command — See: riffing. 2. Write a custom command — See: finger exercises. G'MIC cognoscenti recognize that riffs and finger exercises are one and the same: riffs harness an automatic generation of custom commands; with finger exercises, those custom commands emerge from a script writer's handiwork. Both schemes hide G'MIC commands from the vicissitudes of shell interpretation. help aside, there's little call for running G'MIC commands directly within shells. Command line interpreters compete with G'MIC over syntactically significant characters. Dueling interpreters — each fighting over the same command line — create no end of confusion. |
So:
$ gmic -input 128,128,1,1,255*x/(w-1)
bash: syntax error near unexpected token `('
bash: syntax error near unexpected token `('
leaves one wondering: what's going on?
The command line interpreter — Bash here, yours may differ — is in charge and gets first dibs on on the command line. It won't start the G'MIC interpreter before it understands that it is being told to start the G'MIC interpreter. Until then, it has to work its way through the command line. Working its way through, it discovers an open parenthetical character and decides that it is in the wrong place. The parentheses may have been intended for G'MIC, but the bash interpreter plays by its own rules — and it plays first.
There is nothing we can do about pecking orders. But we can leverage command line rules to our advantage. Nearly every command line interpreter takes single quotes ( '…' ) as delimiters for items that are to be passed — as-is — to the command itself. G'MIC's run command takes advantage of this protocol:
$ gmic -verbose + -run '-input 150,150,1,1,255*x/(w-1)'
[gmic]./ Start G'MIC interpreter (v.3.3.3).
[gmic]./ Increment verbosity level (set to 2).
[gmic]./run/ Import custom commands from expression '__run : -input 150,150,1,1,255*x/(w-1)' (1 new, total: 4675).
[gmic]./run/ Set local variable 'v=1'.
[gmic]./run/ Set verbosity level to 3.
[gmic]./run/__run/ Input image at position 0, with values '255*x/(w-1)' (1 image 150x150x1x1).
[gmic]./run/ Set verbosity level to 1.
[gmic]./run/ Discard definition of custom command '__run' (1 found, 4674 commands left).
…
[gmic]./ Start G'MIC interpreter (v.3.3.3).
[gmic]./ Increment verbosity level (set to 2).
[gmic]./run/ Import custom commands from expression '__run : -input 150,150,1,1,255*x/(w-1)' (1 new, total: 4675).
[gmic]./run/ Set local variable 'v=1'.
[gmic]./run/ Set verbosity level to 3.
[gmic]./run/__run/ Input image at position 0, with values '255*x/(w-1)' (1 image 150x150x1x1).
[gmic]./run/ Set verbosity level to 1.
[gmic]./run/ Discard definition of custom command '__run' (1 found, 4674 commands left).
…
 |
| A left-to-right, black-to-white, ramp |
With such trickery in place, the bash interpreter invokes G'MIC with four items: the verbose command with its + argument, to better see the turning of the trick, then the run command with its pipeline argument — to our eyes. But to the bash interpreter, it is just some ( '…' ) delimited string, something the bash interpreter is not allowed to interpret. With those four items in play, the bash interpreter invokes the "gmic" command, passes the argument list to it and retires from play.
Once invoked, G'MIC takes ownership of that argument list. It finds the run command and the string argument comprising the pipeline. The run command converts that argument into a temporary G'MIC custom command and runs it, for it is now safe from command line interpretation.
Yes — a more roundabout game now. That's OK. This is not performance coding but an exploration. We want to study the G'MIC interpreter without all those other damn interpreters butting in.
Riffing
With dueling interpreters behind us, let's riff — the G'MIC equivalent to improvisational jazz.Here's the play. G'MIC has something like over nine hundred commands — with community contributions thrown in, maybe over a thousand. You, starting out, know what? Could be a dozen? Can't be blamed for not knowing where to begin.
Begin with riffs.
Riffs embody full-on play. As in, being four years old and in a sandbox. Nobody tells you what to do. Nor do you do much strategic planning. You just do whatever floats into your head, and the notions and whimsies and bits of caprice that do float in interconnect with the bits already there, concocting a cognitive brew.
Reading tutorials — as you are doing now — can help, insofar as tutorials point out possibilities, here and there. But if you are going to slay dragons, then at some point you are going to have to put that book down about slaying dragons, go out, and slay dragons. Good luck with that. At least with G'MIC there are no complications with forgetting your mace.
So. Let's riff. To the left-to-right ramp that we have already worked out let's apply a Hue, Saturation and Value (hsv) map. Why? Well, why not? Some tutorial said stuff-and-feathers about how it takes "luminosity scalars to RGB vectors" — what is that about, really?
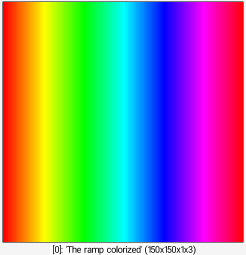 |
| The ramp colorized |
$ gmic -run '150,150,1,1,255*x/(w-1) -map hsv'
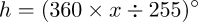 , fix saturation and value to one and display the follow-on HSV triplet in its corresponding RGB form. To be sure, map hsv doesn't actually go through such calculations for every x. It does a table look-up of pre-computed RGB values. And, in the main, that is how all the mappings work: from scalar-to-color by what could be an arbitrarily composed look-up table: the palette.
, fix saturation and value to one and display the follow-on HSV triplet in its corresponding RGB form. To be sure, map hsv doesn't actually go through such calculations for every x. It does a table look-up of pre-computed RGB values. And, in the main, that is how all the mappings work: from scalar-to-color by what could be an arbitrarily composed look-up table: the palette.So that's mapping. Now lets snowball the riff. To what we have, add the apply_curve command. Tutorials claims it changes the "luminosity transfer function". What the H-E-Double Tooth Picks is that?
Um. Well, Take some (O,N) pairs, and a "smoothing argument" S — here, one, for maximum smoothing, but ranging to zero, for not smoothing at all. The O's are "old" values taken from the ramp; the N's are new values. The pairs specify transfer values, a few samples which apply_curve interpolates. Such an interpolation generates the full transfer function.
![d=0,64,200,64,0 150,150,1,1,255*x/(w-1) =>. linear i ($d) display_graph. 300,300,2,4,0,255,0,255 =>. transfer r2dx[transfer] 50% +apply_curve[linear] 1,0,0,63,64,127,200,191,64,255,0 =>. bellcurve +map. hsv =>. hsv_bellcurve to_rgb[linear,transfer,bellcurve,hsv_bellcurve] _parse_cli_images append x r2dx. 50%](img/d_0_64_200_64_0_150_150_1_1_255_x_w_1_linear_i_d_display_graph_300_300_2_4_0_255_0_255_transfer_r2dx_transfer_50_apply_curve_linear_1_0_0_63_64_127_200_191_64_255_0_bellcurve_map_hsv_hsv_bellcurve.png) |
| The ramp is now not-a-ramp (aka — a bellcurve) |
$ gmic -run '-input 150,150,1,1,255*x/(w-1) -apply_curve. 1,0,0,63,64,127,200,191,64,255,0 -map. hsv
Let's snowball the riff even more. What do maps other than hsv look like? Let's find out:
![150,150,1,1,255*x/(w-1) -apply_curve. 1,0,0,63,64,127,200,191,64,255,0 -name. bellcurve +map[bellcurve] balance -name. balance +map[bellcurve] aurora -name. aurora +map[bellcurve] jet -name. jet _parse_cli_images a x r2dx. 50%](img/_150_150_1_1_255_x_w_1_apply_curve_1_0_0_63_64_127_200_191_64_255_0_name_bellcurve_map_bellcurve_balance_name_balance_map_bellcurve_aurora_name_aurora_map_bellcurve_jet_name_jet_parse_cli_images_a.png) |
-![150,150,1,1,255*x/(w-1) -apply_curve. 1,0,0,63,64,127,200,191,64,255,0 -name. bellcurve +map[bellcurve] curl -name. curl +map[bellcurve] hocuspocus -name. hocuspocus +map[bellcurve] rain -name. rain +map[bellcurve] matter -name. matter rm[bellcurve] _parse_cli_images a x r2dx. 50%](img/_150_150_1_1_255_x_w_1_apply_curve_1_0_0_63_64_127_200_191_64_255_0_name_bellcurve_map_bellcurve_curl_name_curl_map_bellcurve_hocuspocus_name_hocuspocus_map_bellcurve_rain_name_rain_map_bellcurve_.png) |
| Multitudes of Mappings |
$ gmic -run '150,150,1,1,255*x/(w-1) -apply_curve. 1,0,0,63,64,127,200,191,64,255,0 -name. bellcurve +map[bellcurve] balance -name. balance +map[bellcurve] aurora -name. aurora +map[bellcurve] jet -name. jet +map[bellcurve] curl -name. curl +map[bellcurve] hocuspocus -name. hocuspocus +map[bellcurve] rain -name. rain +map[bellcurve] matter -name. matter'
From this riff we have a takeaway: name, a way to "bookmark" images. Label an image, say "bellcurve", then refer to it in lots of elsewheres. Don't worry about what stack position "bellcurve" may have at the moment. It retains its label even as its position shifts. Such signposts make easy work of referring to a master image, "bellcurve", in a bevy of -map commands.
Snowballing some more with exclusive OR's:
![150,150,1,1,255*x/(w-1) name. linear +apply_curve[linear] 1,0,0,63,64,127,200,191,64,255,0 name. bellcurve +map[bellcurve] balance name. balance +rotate[linear] 90 name. delta apply_curve[delta] 1,0,0,63,200,127,127,191,10,255,200 map. delta +xor[balance,delta] name. MagicCarpet _parse_cli_images a x r2dx. 50%](img/_150_150_1_1_255_x_w_1_name_linear_apply_curve_linear_1_0_0_63_64_127_200_191_64_255_0_name_bellcurve_map_bellcurve_balance_name_balance_rotate_linear_90_name_delta_apply_curve_delta_1_0_0_63_200_.png) |
| XORing a Magic Carpet |
$ gmic -run '-input 150,150,1,1,255*x/(w-1) -name. linear +apply_curve[linear] 1,0,0,63,64,127,200,191,64,255,0 -name. bellcurve +map[bellcurve] balance -name. balance +rotate[linear] 90 -name. delta -apply_curve[delta] 1,0,0,63,200,127,127,191,10,255,200 -map. delta +xor[balance,delta] -name. MagicCarpet'
From this riff, another takeaway. These - and + specialization prefixes manage how commands treat selected images. - engenders the replacement of selected images with their command-transformed versions. + leaves the selected images unchanged; transformed versions appear at the end of the image list. Omit specializations for replacement behavior. Astutely, then, - has no constructive use; its presence wholly serves readability. When present, it distinguishes commands in the fog of a long pipeline. Omit for brevity; include for lucidity.
Lets snowball some more — with a sprinkling of rotational and circular commands:
![150,150,1,1,255*x/(w-1) polar2euclidean 50%,50% name. circle apply_curve[circle] 1,0,0,63,64,127,200,191,64,255,0 resize[circle] 60%,100%,100%,100%,5,1 expand_x[circle] {w/3},2 +map[circle] balance name. balance rotate[balance] 57,2,1,50%,50% +apply_curve[circle] 1,0,0,63,30,127,250,191,64,255,0 map. delta name. delta rotate[delta] -27,2,1,50%,50% +blend[balance] [delta],difference,1,0 name. "Difference Ellipses" normalize 0,255 _parse_cli_images a x r2dx. 50%](img/_150_150_1_1_255_x_w_1_polar2euclidean_50_50_name_circle_apply_curve_circle_1_0_0_63_64_127_200_191_64_255_0_resize_circle_60_100_100_100_5_1_expand_x_circle_w_3_2_map_circle_balance_name_balance_.png) |
| Differencing Ellipses |
$ gmic -run '-input 150,150,1,1,255*x/(w-1) -polar2euclidean 50%,50% -name. circle -apply_curve[circle] 1,0,0,63,64,127,200,191,64,255,0 -resize[circle] 60%,100%,100%,100%,5,1 -expand_x[circle] {w/3},2 +map[circle] balance -name. balance -rotate[balance] 57,2,1,50%,50% +apply_curve[circle] 1,0,0,63,30,127,250,191,64,255,0 -map. delta -name. delta -rotate[delta] -27,2,1,50%,50% -blend[balance] [delta],difference,1,0 -remove[^balance] -normalize 0,255 -name. DifferenceEllipses'
That's one branch of activity; we name the image at its tip "balance", after the mapping that gave it its color. It is a nice name. We might remember it long enough to use it again. Ah! Speaking of remembering names, remember "circle"? Where we put the peg? Do a duplication specialization of that circle image, piling a second apply_curve on top of the first because applying bell curves on top of bell curves is cheap way to frequency double. Honest.
To that frequency-doubled confection, we map its gray scale pels to RGB pixels using the "delta" palette. That we rotate –27° because we can — and — heck! — who's to stop us? Pound another peg into the ground; call this latest confection "delta". That brings us to the Grande Finale!!! We blend "balance" over "delta" using the difference blending function, opacity full on, clean up with a 0-255 normalization, sweep the image list of all but the finale — The ^ prefix in selections means everything but — call that "DifferenceEllipses." aaaaaannnnnd — we're done!
You got all that?
Didn't think so.
And there be the rub with riffs. Vocabulary building by way of riffs comes from piling on riffs. The first attempts with short riffs yield a little knowledge. Pile on riffs, and, through the cross-pollination of ideas, a little knowledge yields even more knowledge: an acceleration of acquired vocabulary.
— But! That only goes so far.
There comes a point when riffs snowball into incomprehensibility. After a night of snowballing, a riff may become Altogether Majestic, but through the next morning's blear, that riff seems to be written in hieroglyphs.
It's not quite a failure in remembering how new-found commands work; it is obfuscation buildup, to which structureless riffs are susceptible. A gigantically snowballed riff hides its purport in a crowd of characters; you can't see meaning for letters.
The solution lies with Finger Exercises
Updated: 16-Decenver-2023 17:30 UTC commit: 3e43b535fb842e69cc968e6d24c166e3889447dc


 Home
Home Download
Download News
News Mastodon
Mastodon Bluesky
Bluesky X
X Summary - 17 Years
Summary - 17 Years Summary - 16 Years
Summary - 16 Years Summary - 15 Years
Summary - 15 Years Summary - 13 Years
Summary - 13 Years Summary - 11 Years
Summary - 11 Years Summary - 10 Years
Summary - 10 Years Resources
Resources Technical Reference
Technical Reference Scripting Tutorial
Scripting Tutorial Video Tutorials
Video Tutorials Wiki Pages
Wiki Pages Image Gallery
Image Gallery Color Presets
Color Presets Using libgmic
Using libgmic G'MIC Online
G'MIC Online Community
Community Discussion Forum (Pixls.us)
Discussion Forum (Pixls.us) GimpChat
GimpChat IRC
IRC Report Issue
Report Issue