luminance
luminance as a relief from the overly loud.
luminance performs a conversion of eight bit color images assumed to be situated the in sRGB space, producing a single channel "panchromatically correct" gray scale image. This notion of panchromatic correctness is grounded on the assumptions that the input image is situated in the sRGB space and that its channels are eight bits deep, each distinguishing 256 intensity levels. The conversion process from sRGB to panchromatic gray takes place in three steps:
| 1. | Gamma expansion takes place for each channel, resulting in "linear RGB": that is, a mapping where one-step changes in intensity, u, lead to identical one-step increases in the perceived brightness of that ideal viewing device – which does not exist anywhere on any known planet. |
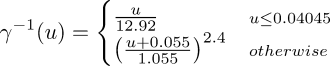
The reverse transform from sRGB to RGB. The gamma expansion function moves highlight detail to lower values of u, shifting highlights at the expense of shadows and making them darker in appearance.
| This piecewise equation is calibrated for intensities u in the interval [0 … 1]. For the first piece, it simply down-scales pixels equal to or darker than 0.04045. For this small interval, simple scaling is a stabler computation than a power function. For the second piece it applies an expansion gamma function. G'MIC harnesses srgb2rgb to convert each channel to linear RGB, applying this gamma transform identically to each. | |
| 2. | Following gamma expansion to linear RGB, G'MIC adds the channels together, using specific weights that partition unity: |
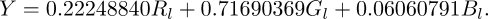
| where Y represents relative illuminance. | |
| 3. | Y is still a "linear gray" however, adapted to the ideal viewing device. To shift this gray to (presumably) real world displays, G'MIC performs a gamma compression step, aligning the gray with sRGB: |
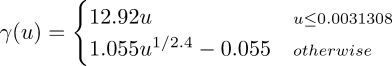
The forward transform from RGB to sRGB. The gamma compression function moves shadow detail to higher values of u, making them lighter in appearance and expanding shadows at the expense of highlights. This approximates the behavior of the human eye.
| As with the reverse transform, a piecewise function performs a simple up-scaling on tiny values, applying a "compression" gamma function to the remainder of the interval. 0.0031308, if you must know, is the RGB-transformed marker of 0.04045 sRGB. G'MIC embodies this forward transform in the command rgb2srgb. |
The linear RGB weights, along with the gamma expansion and compression gamma functions, stem from the International Telecommunication Union's specification BT.709-2 for HDTV broadcast television, which original sRGB sponsors Microsoft and Hewlett-Packard adopted for modeling the behavior of the typical 8-bit/channel computer display. Informally, gray stems from the green channel, with small and negligible contributions, respectively, from red and blue.
Whether this pedigreed conversion of luminance fits one's aesthetics of gray – or not – is a discussion for another day. Keep luminance in your kit as the standards-based color to gray converter. So long as its input has three channels, each in the intensity range of 8-bit color, 0-255, each (presumably) gamma-compressed to fit the sRGB scheme of shadow-enhanced illuminance, then luminance will output a grayscale analog image also in the 8-bit range, also compatible with sRGB, without any clipping of the luminance range.
What about other input? If luminance encounters an alpha channel – or any input image in excess of three channels – it will harness remove_opacity to strip the highest-numbered channel, presumed to be an alpha channel. If the channel count still exceeds three, the command will not perform the pedegreed conversion but punts instead: harnessing norm as a gray scale converter. norm generates grays by different principles, regarding image channels as vector components and equating gray to their Euclidean length. Without normalization, it's likely that such lengths will exceed the 0-255 luminance range of eight bit channels. luminance will also harness norm if it encounters two channel images. However, the command simply leaves one channel images unchanged; it assumes that such are already gray-scaled.
Consider using to_gray or to_graya, for images with alpha channels, if the lenience of luminance doesn't fit well in your batch processing schemes. These are wrappers around luminance, with checks to reject out-of-band inputs. This prevents luminance from using its norm-based pathways. Harness onfail endowed local … done blocks to drop rejected images without halting processing.
Sixteen bit or floating point channels also do not fare well with luminance; gamma compression and expansion commands, rgb2srgb and rgbs2rgb presently use a hard-wired 255.0 scaling factor to go to and from [0 … 1] luminance ranges. This is not oversight. Strictly speaking, sRGB is an 8-bit-based color space designed for 24-bit three-color displays. RGB images with sixteen bit deep channels are very nearly white after being mangled by luminance, perhaps another useful antidote to loud, overly-saturated ties and those who wear them.
Command reference
$ gmic -h luminance
luminance:
Compute luminance of selected sRGB images.
Example:
[#1] image.jpg +luminance
Tutorial: https://gmic.eu/tutorial/luminance
luminance:
Compute luminance of selected sRGB images.
Example:
[#1] image.jpg +luminance
Tutorial: https://gmic.eu/tutorial/luminance


 Home
Home Download
Download News
News Mastodon
Mastodon Bluesky
Bluesky X
X Summary - 17 Years
Summary - 17 Years Summary - 16 Years
Summary - 16 Years Summary - 15 Years
Summary - 15 Years Summary - 13 Years
Summary - 13 Years Summary - 11 Years
Summary - 11 Years Summary - 10 Years
Summary - 10 Years Resources
Resources Technical Reference
Technical Reference Scripting Tutorial
Scripting Tutorial Video Tutorials
Video Tutorials Wiki Pages
Wiki Pages Image Gallery
Image Gallery Color Presets
Color Presets Using libgmic
Using libgmic G'MIC Online
G'MIC Online Community
Community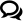 Discussion Forum (Pixls.us)
Discussion Forum (Pixls.us) GimpChat
GimpChat IRC
IRC Report Issue
Report Issue