A Full-Featured Open-Source Framework for Image Processing

Images as Data Sets

First and formost, G'MIC is a research tool. Many commands routinely produce images which are useful data sets, but do not span a range of values compatible with standard graphic file formats. Commonly, display will normalize such data sets so that your computer screen will show something, but the output command will not concomitantly write normalized data to the file. For all that G'MIC knows, you may want your data set in a non-standard range.

The display command does report a set of metrics for each image in the pipeline following the summary lines. Of particular interest are the maximum and minimum pixel values of each image. Some commands produce pixels that exceed the so-called normal range of image formats and, if output, these files will not work in other programs. One should always review the image metrics as well as the display window to ensure that an image is within the norms expected for the output format.

For example, we may harness the bandpass command to get only the very low frequency content of an image. Artistically, it furnishes a very distinctive pattern.

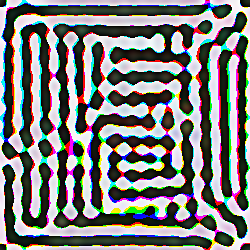How the display command depicts the output of the bandpass command	How the output command writes bandpass data to disk

Pixel row 177, (red channel). Green curve: data from the left image, as it originally was in the image stack. Red curve: data from the right image, as it was written to disk

In this example, the data set resulting from the -bandpass command ranged from a minimum of -83.5938 – blacker than black – to a maximum of 93.4782. Following on, the -output command wrote a PNG file.

It so happens that PNG files usually consist of eight or sixteen bits per channel unsigned integers that range from 0 to 255 for eight bits or 0 to 65535 for sixteen bits. In the example, a default conversion from floating point to unsigned integers took place: so-called 'blacker than black' pixels, negative quantities, wrapped around to positive quantities, because, by definition, negative numbers cannot be represented in unsigned integer formats. In the conversion from floating point to unsigned integers, signed integers are an intermediary form. Negative signed integers are written in two's complement, with the most significant bit representing the sign and set to one to indicate a value less than zero. In eight bit channels, -1 has the two's complement representation of 11111111. This bit pattern has a very different meaning as an unsigned eight bit integer. In that interpretation, the most significant bit is not a sign, but represents the 27 binary place, 1111111 represents 255 among unsigned eight bit integers, not -1. In effect, the literal bit patterns are written to disk, but not the signed/unsigned interpretation. But for the width of the data channel, similar circumstances prevail for sixteen bit unsigned integer channels.

Opening the PNG file in one's favorite paint program gives rise to surprising results, all the 'blacker than black' intensities represented in the G'MIC preview as dark shades appear white or nearly white in one's favorite paint program, the conversion of negative 'blacker than black' values wrapping around through the virtual addition of  256, for eight bits, or 65,536 for sixteen bit files.

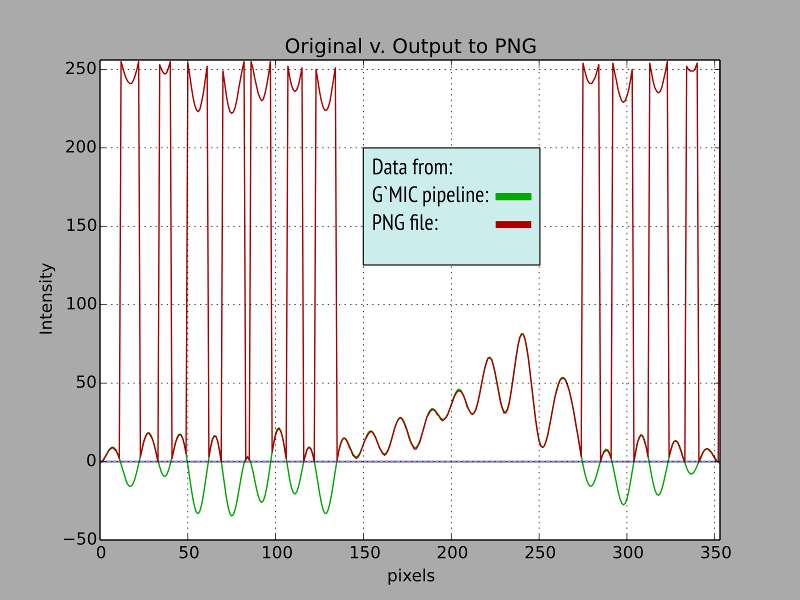
To visualize this, we graphed the red channel from one scan line of the example as it was originally in the image stack, and again after it was written to file encoded as unsigned eight bit integers. The green curve depicts the original data; the red depicts data on disk after conversion. So long as the original data were positive, the eight bit unsigned numerals on disk tracked their original floating point counterparts fairly closely, with only minor rounding error. Where the original data are negative, however, the corresponding file quantities swing abruptly positive, offset from the original by exactly 256. The blacker-than-black' values wrap around to white or very nearly white.

Visually, the data in the file is quite different than what the -display command showed. And yet, nothing is broken. Every command is strictly doing what it has been designed to do. The difficulty is that what they have been designed to do is not what we want. To really get what we want, we have to prepare data sets to be stored in standard graphic files, that is, knowing that a particular output format consists of unsigned integers ranging from 0 to 255. We then have to decide how to scale and offset data in a way that doesn't (much) change the data's visual representation.

Data Management

G'MIC commands have no knowledge (or concern) about the bandwidth of outputs. To give people some idea about what is going on, the G'MIC ' -display command implicitly normalizes pixel values to a range that the screen can accomodate, typically 0 – 255. This alteration can give rise to display values which are very different than the image stack values. To bridge this mismatch, the mouse pointer reports the actual pixel values as stored in G'MIC's image stack when the -display command is active and a specific image is selected.

At the end of the day, however, some decision needs to be made about an image being written to a file. The common choices are:

  1. Nothing
  2. Cut
  3. Normalize

Nothing

Nothing is pretty easy. G'MIC has its own native format, cimg, named after its core image processing library. It is a very simple, very accommodating format that will, as much as humanly possible, preserve numerical data - it stores pixels as floating point numerals, preserving the sign and as much of the precision of the data as the floating point format allows. It is also a multi-image format; an undecorated output command will write the entire image stack to one .cimg file. This is the best choice when you know you are not ready to display data as images yet, that you may very well have other operations in mind; maybe you aren't quite sure what those operations are yet. Writing the image stack out to a .cimg file essentially puts the entire stack on ice. Later on, when you know what you want to do with the data, you can input the .cimg file of your iced image stack and pick up where you left off. Writing a .cimg file is easy: simply name a file with a .cimg extension and the output command will do the rest.

The difficulty with doing nothing is that you probably can't display the data without distorting it in some fashion, and you most likely can't hand it off to a graphics program. If you are bent on displaying a data set, then you need to make some choices about the out-of-band values, i. e. those that fall outside of 0 – 255 for an eight bit PNG file. That is what the remaining choices are for.

Cut

If your image has pixels with channel values less than zero or greater than what your file format can accommodate, you can clip out-of-bounds data with the cut command, which takes a bottom and top clipping values. Pixel channel values falling below the lower bound are set to that boundary value. Similarly, pixel channel values above the upper bound are set to that value. The upside is that intermediary values are not changed, so channel values and the colors they form are undisturbed. The downside is that details conveyed by out of band channel values will be flattened to one or the other boundary and be lost.

Normalize

If details matter, the G'MIC normalize command may be harnessed to adjust minimum and maximum values to match the minimum and maximum values of the destination file format. The channel values stored in the file will be scaled to fit within the lower and upper boundaries, to wit: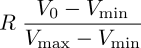

where 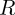is a desired upper boundary value and where zero will be the implied lower boundary value. You pick 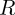to be apt for the destination file, 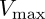and 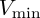represent the largest and smallest channel values present in a pre-normalized image, and 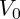is a pre-normalized channel value of a pixel in need of adjustment. This ratio scales 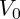to a normalized value which will fall within 0.0 and 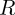inclusive. This scheme will preserve details so long as the dynamic range of the original is not vastly larger than 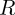. but original color relationships in will necessarily change.

The normalize command is not a panacea for all out-of-band ills, however. Images with high dynamic ranges would be ruined if constrained to eight bit unsigned integers; in this case, the EXR image format might be a better choice.

---

Updated: 07-May-2023 20:40 UTC Commit: 79f1223f76abc9d217cab05bf38ca89560b76ee6