A Full-Featured Open-Source Framework for Image Processing

for (+)

The -for <loop scope> -done commands form a syntactical unit that repeatedly tests the mathematical expression argument given to -for and, if True, executes the in-scope commands, if any. The <loop scope> need not be populated and is a placeholder when empty. -for…-done expresses a "test, then perform" pattern. With the conditional test at the top of the loop, the in-scope commands won't execute at all if -for's argument first resolves to False. For a "perform, then test" pattern. consider do … while. If the contemplated conditional test entails simply incrementing or decrementing a counter, consider -repeat…-done instead, which has such counters built in. -for…-done is better for less straight forward circumstances, such reacting to changes in image conditions. Prior to 2.6, -for would test file system references. This is no longer supported. Use the file system mathematical expressions isfile() or isdir() instead.

Examples

One common use entails running a process until an image metric reaches a certain value. With -convolveuntil we repeatly convolve-and-normalize an image containing unit impulses with an (approximate) Airy disk. This particular kernel amplifies differences in images.

convolveuntil:      -300,300,1,1            # Zero image with unit impulses.     -noise 0.01,2      -abs.      -input 3,3,1,1,-0.125   # 3×3 Airy Disk for      -set. 1,1,1             # repeated convolutions.     -for abs(im#-2)<=0.72   # Convolve until image        -convolve.. [-1],2,1 # minimum falls to -0.72.     -done      -remove.      -normalize. 0,255

Variance: Dispersion From The Expected

Informally, Variance reflects the dispersion of observed values from an expected value, often, but not necessarily, their collective average — even more informally, their "sprawl". For example, if all observed values equal the expected value then there is no dispersal and the variance is zero.

On the other extreme, where there are only black (0) or white (1) values, the expected value of the ensemble may very well be one half, but nary an observation actually fits such a value; they fall to one extreme or the other. In this example, the variance is 0.25 and stems from how the variance of an ensemble is computed:


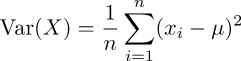
where µ is the expected value and the xi are instances from the ensemble of n observed values. If we take the expected value to be the image mean, then both black and white observations vary from this mean by 0.5 absolute. The average of these squared differences is 0.25. Note that an "expected value" is just that: an observer's wish about ensembles, possibly untethered from any reality. A large variation could then serve as the observer's reality check.

With some squinting, a decrease in variance from an initial reference value could reflect the amount of blurring that has been applied to an image, with a blurred-beyond-any-hope-of-redemption coinciding with a variance of zero. -bluruntil produces a decay curve illustrating how a successively blurred image trends toward an unvarying tonality, though it may never reach variance zero. The command accepts (1) the length of one side of a square test image, not otherwise shown (2) the number of times to blur the test image (3) a target "fully decayed variance", (4) the arguments one would pass to -blur. The command either stops when the specified variance decays to the target variance or the number of blur attempts reaches the number of trials we wish to attempt. These last two tests constitute the heart of a math expression which we present as an argument to -for. See the following:

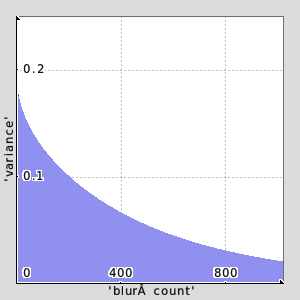bluruntil: check "isint(${1=128})>0 && \                     isint(${1=128})>0 && \                     isnum(${3=1})>0   && \                     isnum(${4=1})>0   && \                     isbool(${5=1})    && \                     isbool(${6=0})"     $=limit_     sigma={0.25*$limit_1}     -input $limit_1,$limit_1,1,1     -name. blurbox     -gaussian[blurbox] $sigma,$sigma,0     -threshold[blurbox] 50%     curvar={stats(#0)[3]}     -input $limit_2,1,1,1     -name. varlist     arycnt=0     -for ($curvar>$limit_3)&&($arycnt<$limit_2)        -blur[blurbox] $limit_4,$limit_5,$limit_6        curvar={stats(#0)[3]}        -set[varlist] $curvar,$arycnt,0,0        arycnt+=1     -done     -display_graph[varlist] 300,300,3

G'MIC computes image variance, where image average ia serves as "expected value", µ, but does not present variance as a part of image summaries. If you must know, the mathematical expression function stats() provides it as the fourth element in the return vector. echo "Variance: "{stats(#0)[3]} at your leisure for the variance of the first image in the list.

Command Reference

Updated: 31-July-2021 11:45 UTC Commit: 731cf95f59cb